
已知椭圆的中心在原点,准线方程为x=±4,如果直线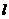 :3x-2y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点.
:3x-2y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点.
(1)求椭圆方程;
(2)设直线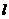 与椭圆的一个交点为P,F是椭圆的一个焦点,试探究以PF为直径的圆与椭圆长轴为直径的圆的位置关系;
与椭圆的一个交点为P,F是椭圆的一个焦点,试探究以PF为直径的圆与椭圆长轴为直径的圆的位置关系;
(3)把(2)的情况作一推广:写出命题(不要求证明).
解:(1)设椭圆方程为 (a>b>0)
(a>b>0)
直线3x-2y=0与椭圆的一个交点的坐标是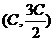 ,代入椭圆方程得:
,代入椭圆方程得:
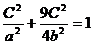 又
又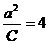 a2=b2+c2
a2=b2+c2
∴ a=2  C=1
C=1
∴ ………………5分
………………5分
(2)由(1)知,直线与椭圆的一个交点为 ,F(1,0),则从PF为直径的圆的方程
,F(1,0),则从PF为直径的圆的方程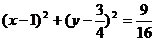 ,圆心为
,圆心为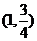 ,半径为
,半径为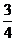
以椭圆长轴为直径的圆的方程为x2+y2=4,圆心(0,0),半径为2
两圆圆心之间距离为
∴ 两圆内切 ………………8分
P、F为其它三种情况时,两圆都为内切 ………………10分
(3)如果椭圆的方程是 (a>b>0),P是椭圆上的任意一点,F是椭圆的一个焦点,则以PF长为直径的圆与以椭圆长轴为直径的圆是内切关系。
…………13分
(a>b>0),P是椭圆上的任意一点,F是椭圆的一个焦点,则以PF长为直径的圆与以椭圆长轴为直径的圆是内切关系。
…………13分
(如P写成椭圆上的定点,此问只给1分)


科目:高中数学 来源: 题型:
| ||
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 25 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com