
| A. | 两个点 | B. | 一个椭圆 | C. | 一条线段 | D. | 两条直线 |
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{4}$ | B. | $\frac{7}{5}$ | C. | $\frac{15}{4}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 2 | C. | -4或-$\frac{1}{4}$ | D. | -2或-$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是某校十大歌手比赛上,七位评委为某同学打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图是某校十大歌手比赛上,七位评委为某同学打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 85,4.84 | B. | 85,1.6 | C. | 86,1.6 | D. | 86,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | $(-1+\sqrt{3},1)∪(-3,-1-\sqrt{3})$ | C. | $(-1-\sqrt{3},-1+\sqrt{3})$ | D. | $(-∞,-1-\sqrt{3})∪(-1+\sqrt{3},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
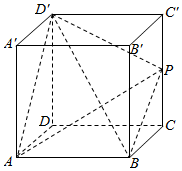 在棱长为4的正方体ABCD-A′B′C′D′中,点P在棱CC′上,且CC′=2CP.
在棱长为4的正方体ABCD-A′B′C′D′中,点P在棱CC′上,且CC′=2CP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com