已知整数列{an}满足a3=-1,a7=4,前6项依次成等差数列,从第5项起依次成等比数列.
(1)求数列{an}的通项公式;
(2)求出所有的正整数m,使得am+am+1+am+2=amam+1am+2.
【答案】
分析:(1)由题意设数列前6项的公差为d,d为整数,表示出a
5,a
6,利用a
5,a
6,a
7成等比数列,求出d,推出n≤6时等差数列的通项公式,n≥5数列{a
n}的通项公式;
(2)验证正整数m=1,2,3,4,时,等式a
m+a
m+1+a
m+2=a
ma
m+1a
m+2是否成立,m≥5时,验证等式的左边的值与右侧的值是否相同即可,得到结论.
解答:解(1)设数列前6项的公差为d,d为整数,则a
5=-1+2d,a
6=-1+3d,d为整数,
又a
5,a
6,a
7成等比数列,
所以(3d-1)
3=4(2d-1),解得d=1,-------4分
当n≤4时,a
n=n-4,
由此a
5=1,a
6=2,数列第5项起构成以2为公比的等比数列.
当n≥5时,a
n=2
n-5,
故通项公式为
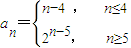
,-------------------------------------8分
(2)由(1)知数列{a
n}为:-3,-2,-1,0,1,2,4,8,16,…
当m=1时等式成立,即-3-2-1=-6=(-3)(-2)(-1);等式成立.
当m=3时等式成立,即-1+0+1=0;等式成立.
当m=2、4时等式不成立;--------------------------------------------------12分
当m≥5时,即a
m+a
m+1+a
m+2=2
m-5(2
3-1),a
ma
m+1a
m+2=2
3m-12.
所以a
m+a
m+1+a
m+2≠a
ma
m+1a
m+2.;
故所求的m=1,或m=3------------------------------------------------------15分
点评:本题考查等比数列的判断,通项公式的求法,考查数列的函数的特征,注意数列的前提条件的应用,注意验证法在解题中的应用,注意分类讨论的思想.

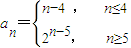 ,-------------------------------------8分
,-------------------------------------8分

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案