
【题目】已知抛物线C的顶点为O(0,0),焦点F(0,1)
(Ⅰ)求抛物线C的方程;
(Ⅱ)过F作直线交抛物线于A、B两点.若直线OA、OB分别交直线l:y=x﹣2于M、N两点,求|MN|的最小值.
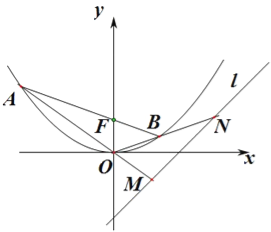
【答案】(1)x2=4y
(2)当t=﹣![]() 时,|MN|的最小值是
时,|MN|的最小值是![]()
【解析】(I)由题意可设抛物线C的方程为x2=2py(p>0)则![]() =1,解得p=2,故抛物线C的方程为x2=4y
=1,解得p=2,故抛物线C的方程为x2=4y
(II)设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+1
由![]() 消去y,整理得x2﹣4kx﹣4=0
消去y,整理得x2﹣4kx﹣4=0
所以x1+x2=4k,x1x2=﹣4,从而有|x1﹣x2|=![]() =4
=4![]()
由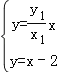 解得点M的横坐标为xM=
解得点M的横坐标为xM=![]() =
=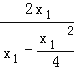 =
=![]() ,
,
同理可得点N的横坐标为xN=![]()
所以|MN|=![]() |xM﹣xN|=
|xM﹣xN|=![]() |
|![]() ﹣
﹣![]() |=8
|=8![]() |
|![]() |=
|=![]()
令4k﹣3=t,t不为0,则k=![]()
当t>0时,|MN|=2![]()
![]() >2
>2![]()
当t<0时,|MN|=2![]()
![]() =2
=2![]()
![]() ≥
≥![]()
综上所述,当t=﹣![]() 时,|MN|的最小值是
时,|MN|的最小值是![]()


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
【题目】因客流量临时增大,某鞋店拟用一个高为50![]() (即
(即![]() )的平面镜自制一个竖直摆放的简易鞋镜,根据经验:一般顾客
)的平面镜自制一个竖直摆放的简易鞋镜,根据经验:一般顾客![]() 的眼睛
的眼睛![]() 到地面的距离为
到地面的距离为![]() (
(![]() )在区间
)在区间![]() 内,设支架
内,设支架![]() 高为
高为![]() (
(![]() )
)![]() ,
,![]() ,顾客可视的镜像范围为
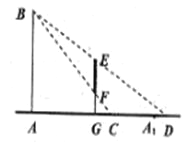
,顾客可视的镜像范围为![]() (如图所示),记
(如图所示),记![]() 的长度为
的长度为![]() (
(![]() ).
).
(I)当![]() 时,试求
时,试求![]() 关于
关于![]() 的函数关系式和
的函数关系式和![]() 的最大值;
的最大值;
(II)当顾客的鞋![]() 在镜中的像
在镜中的像![]() 满足不等关系
满足不等关系![]() (不计鞋长)时,称顾客可在镜中看到自己的鞋,若使一般顾客都能在镜中看到自己的鞋,试求
(不计鞋长)时,称顾客可在镜中看到自己的鞋,若使一般顾客都能在镜中看到自己的鞋,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解高校学生平均每天使用手机的时间长短是否与性别有关,某调查小组随机抽取了25 名男生、10名女生进行为期一周的跟踪调查,调查结果如表所示:
平均每天使用手机 | 平均每天使用手机 | 合计 | |
男生 | 15 | 10 | 25 |
女生 | 3 | 7 | 10 |
合计 | 18 | 17 | 35 |
(I)在参与调查的平均每天使用手机不超过3小时的7名女生中,有4人使用国产手机,从这7名女生中任意选取2人,求至少有1人使用国产手机的概率;
(II) 根据列联表,是否有90%的把握认为学生使用手机的时间长短与性别有关(![]() 的观测值
的观测值![]() 精确到0.01).
精确到0.01).
附:
| 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
参考公式: 
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在给出的下列命题中,正确的是( )
A.设![]() 是同一平面上的四个点,若
是同一平面上的四个点,若![]() ,则点
,则点![]() 必共线
必共线
B.若向量![]() 是平面
是平面![]() 上的两个向量,则平面
上的两个向量,则平面![]() 上的任一向量
上的任一向量![]() 都可以表示为
都可以表示为![]() ,且表示方法是唯一的
,且表示方法是唯一的
C.已知平面向量![]() 满足
满足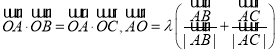 则
则![]() 为等腰三角形
为等腰三角形
D.已知平面向量![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 是等边三角形
是等边三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( )

A. 互联网行业从业人员中90后占一半以上
B. 互联网行业中从事技术岗位的人数超过总人数的![]()
C. 互联网行业中从事运营岗位的人数90后比80前多
D. 互联网行业中从事运营岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某田径队有三名短跑运动员,根据平时训练情况统计甲、乙、丙三人100米跑(互不影响)的成绩合格的概率分别为![]() ,
,![]() ,
,![]() ,若对这三名短跑运动员的100米跑的成绩进行一次检测.
,若对这三名短跑运动员的100米跑的成绩进行一次检测.
(1)求三人都合格的概率;
(2)求三人都不合格的概率;
(3)求出现几人合格的概率最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学家欧拉在1765年提出,任意三角形的外心、重心、垂心位于同一条直线上,后人称这条直线为欧拉线.已知△ABC的顶点A(2,0),B(0,4),若其欧拉线的方程为x-y+2=0,则顶点C的坐标为
A. (-4,0) B. (-3,-1) C. (-5,0) D. (-4,-2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() 、
、![]() ,
,![]() 为椭圆
为椭圆![]() 的一个短轴顶点,
的一个短轴顶点,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若经过椭圆![]() 左焦点的直线
左焦点的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,
两点,![]() 为椭圆
为椭圆![]() 的右顶点,求
的右顶点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com