
【题目】如图,在正四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,下列四个结论不成立的是 ( )
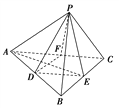
A. BC∥平面PDF B. DF⊥平面PAE
C. 平面PDF⊥平面PAE D. 平面PDE⊥平面ABC
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,下列说法错误的是( )
,下列说法错误的是( )
A. 若![]() 有最大值,则
有最大值,则![]() 也有最大值
也有最大值
B. 若![]() 有最大值,则
有最大值,则![]() 也有最大值
也有最大值
C. 若数列![]() 不单调,则数列
不单调,则数列![]() 也不单调
也不单调
D. 若数列![]() 不单调,则数列
不单调,则数列![]() 也不单调
也不单调
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为打入国际市场,决定从![]() 两种产品中只选择一种进行投资生产.已知投资生产这两种产品的有关数据如下表:(单位:万美元)
两种产品中只选择一种进行投资生产.已知投资生产这两种产品的有关数据如下表:(单位:万美元)

其中年固定成本与年生产的件数无关,![]() 为待定常数,其值由生产
为待定常数,其值由生产![]() 产品的原材料价格决定,预计
产品的原材料价格决定,预计![]() .另外,年销售
.另外,年销售![]() 件
件![]() 产品时需上交
产品时需上交![]() 万美元的特别关税.假设生产出来的产品都能在当年销售出去.
万美元的特别关税.假设生产出来的产品都能在当年销售出去.
(1)写出该厂分别投资生产![]() 两种产品的年利润
两种产品的年利润![]() 与生产相应产品的件数
与生产相应产品的件数![]() 之间的函数关系,并指明其定义域;
之间的函数关系,并指明其定义域;
(2)如何投资才可获得最大年利润?请你做出规划.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设H1(x)=max![]() ,H2(x)=min
,H2(x)=min![]() (max
(max![]() 表示p,q中的较大值,min
表示p,q中的较大值,min![]() 表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
A.16B.-16
C.a2-2a-16D.a2+2a-16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)=(a-x)|x|,常数a∈R,且关于x的不等式mx2+m>f[f(x)]对所有的x∈[-2,2]恒成立,则实数m的取值范围是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com