
| lim |
| n���� |
| Sn |
| Sn+1 |
| 2 |
| 3 |
| sn |
| sn+1 |
| bn+1 |
| bn |
| a(1-a2n) |
| 1-a2 |
| Sn |
| Sn+1 |
| 1-a2n |
| 1-a2n+2 |
| lim |
| n���� |
| Sn |
| Sn+1 |
| lim |
| n���� |
| Sn |
| Sn+1 |
| lim |
| n���� |
| 1-a2n |
| 1-a2n+2 |
| lim |
| n���� |
| ||
|
| 1 |
| a2 |
| lim |
| n���� |
| Sn |
| Sn+1 |
|
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
|
|
| 4 |
| 9 |
| 4 |
| 9 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��09�������ʼ��ģ���12�֣�
��֪��A��1��0����B��0��1���ͻ�����ͬ�ĵ�P1��P2��P3������Pn����������
![]() �ǹ��Ϊ��ĵȲ����У�
�ǹ��Ϊ��ĵȲ����У�![]() Ϊ�ȱ����У�OΪ����ԭ�㣬��P1���߶�AB���е㡣
Ϊ�ȱ����У�OΪ����ԭ�㣬��P1���߶�AB���е㡣
��I����![]() ��ֵ��
��ֵ��
��II����![]() �ܷ���ͬһ��ֱ���ϣ�֤����Ľ��ۡ�
�ܷ���ͬһ��ֱ���ϣ�֤����Ľ��ۡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011���Ϻ��г������߿���ѧһģ�Ծ����Ŀƣ��������棩 ���ͣ������
 ��
�� ʱ���ʡ�OPnQn������Ƿ�������ֵ�������ڣ�������ֵ���������ڣ���˵�����ɣ�
ʱ���ʡ�OPnQn������Ƿ�������ֵ�������ڣ�������ֵ���������ڣ���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011��㶫ʡ�߿���ѧģ�����Ծ��������������棩 ���ͣ������
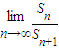 ��
�� ʱ���ʡ�OPnQn������Ƿ�������ֵ�������ڣ�������ֵ���������ڣ���˵�����ɣ�
ʱ���ʡ�OPnQn������Ƿ�������ֵ�������ڣ�������ֵ���������ڣ���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011���Ϻ��г������߿���ѧһģ�Ծ������ƣ��������棩 ���ͣ������
 ��
�� ʱ���ʡ�OPnQn������Ƿ�������ֵ�������ڣ�������ֵ���������ڣ���˵�����ɣ�
ʱ���ʡ�OPnQn������Ƿ�������ֵ�������ڣ�������ֵ���������ڣ���˵�����ɣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com