
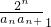 ,设数列{bn}的前n项和为Tn,求使不等式
,设数列{bn}的前n项和为Tn,求使不等式 -Tn<
-Tn< 成立的最小正整数n的值.
成立的最小正整数n的值.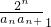 =
= •
•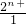 =
= •
•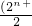 =
= (
(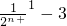 -
-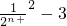 ),
), [(
[(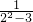 -
-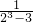 )+(
)+(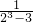 -
-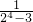 )+…+(
)+…+(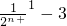 -
-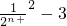 )]
)] ×(
×(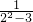 -
-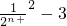 )=
)= -
-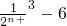 ,
, -Tn=
-Tn=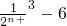 <
< ,即2n+3>2016,故只要n+3≥11,即n≥8,
,即2n+3>2016,故只要n+3≥11,即n≥8,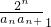 ,利用裂项相消法即可求得数列{bn}的前n项和为Tn,解此不等式
,利用裂项相消法即可求得数列{bn}的前n项和为Tn,解此不等式 -Tn<
-Tn< 即可求得结果.
即可求得结果.

 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com