
【题目】已知函数f(x)=x2﹣2ax(a>0).
(1)当a=2时,解关于x的不等式﹣3<f(x)<5;
(2)对于给定的正数a,有一个最大的正数M(a),使得在整个区间[0,M(a)]上,不等式|f(x)|≤5恒成立.求出M(a)的解析式;
(3)函数y=f(x)在[t,t+2]的最大值为0,最小值是﹣4,求实数a和t的值.
【答案】
(1)解:当a=2时,函数f(x)=x2﹣4x,
∴不等式﹣3<f(x)<5可化为﹣3<x2﹣4x<5,
解得 ![]() ,
,
∴不等式的解集为(﹣1,1)∪(3,5)
(2)解:∵a>0时,f(x)=x2﹣2ax=(x﹣a)2﹣a2,
∴当﹣a2<﹣5,即a> ![]() 时,
时,
要使|f(x)|≤5在x∈[0,M(a)]上恒成立,
要使得M(a)最大,M(a)只能是x2﹣2ax=﹣5的较小的根,
即M(a)=a﹣ ![]() ;
;
当﹣a2≥﹣5,即0<a≤ ![]() 时,
时,
要使|f(x)|≤5在x∈[0,M(a)]上恒成立,
要使得M(a)最大,M(a)只能是x2﹣2ax=5的较大的根,
即M(a)=a+ ![]() ;
;
综上,M(a)= ![]()
(3)解:f(x)=(x﹣a)2﹣a2(t≤x≤t+2),显然f(0)=f(2a)=0.
①若t=0,则a≥t+1,且f(x)min=f(a)=﹣4,或f(x)min=f(2)=﹣4,
当f(a)=﹣a2=﹣4时,a=±2,a=﹣2不合题意,舍去
当f(2)=4﹣4a=﹣4时,a=2,
②若t+2=2a,则a≤t+1,且f(x)min=f(a)=﹣4,或f(x)min=f(2a﹣2)=﹣4,
当f(a)=﹣a2=﹣4时,a=±2,若a=2,t=2,符合题意;
若a=﹣2,则与题设矛盾,不合题意,舍去
当f(2a﹣2)=﹣4时,a=2,t=2
综上所述,a=2,t=0和a=2,t=2符合题意
【解析】(1)a=2时,把不等式﹣3<f(x)<5化为不等式组﹣3<x2﹣4x<5,求出解集即可;(2)由二次函数的图象与性质,讨论a>0时|f(x)|≤5在x∈[0,M(a)]上恒成立时,M(a)最大,此时对应的方程f(x)=±5根的情况,从而求出M(a)的解析式;(3)f(x)=(x﹣a)2﹣a2(t≤x≤t+2),显然f(0)=f(2a)=0,分类讨论,利用y=f(x)在[t,t+2]的最大值为0,最小值是﹣4,求实数a和t的值.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别是AB,BC的中点.将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P. 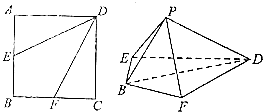
(1)求证:平面PBD⊥平面BFDE;
(2)求二面角P﹣DE﹣F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数F(x)= ![]() ,(a为实数).
,(a为实数).
(1)根据a的不同取值,讨论函数y=f(x)的奇偶性,并说明理由;
(2)若对任意的x≥1,都有1≤f(x)≤3,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:对任意的n∈N*均有an+1=kan+3k﹣3,其中k为不等于0与1的常数,若ai∈{﹣678,﹣78,﹣3,22,222,2222},i=2,3,4,5,则满足条件的a1所有可能值的和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合Ma={f(x)|存在正实数a,使得定义域内任意x都有f(x+a)>f(x)}.
(1)若f(x)=2x﹣x2 , 试判断f(x)是否为M1中的元素,并说明理由;
(2)若 ![]() ,且g(x)∈Ma , 求a的取值范围;
,且g(x)∈Ma , 求a的取值范围;
(3)若 ![]() (k∈R),且h(x)∈M2 , 求h(x)的最小值.
(k∈R),且h(x)∈M2 , 求h(x)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C以原点为中心,左焦点F的坐标是(﹣1,0),长轴长是短轴长的 ![]() 倍,直线l与椭圆C交于点A与B,且A、B都在x轴上方,满足∠OFA+∠OFB=180°;
倍,直线l与椭圆C交于点A与B,且A、B都在x轴上方,满足∠OFA+∠OFB=180°; 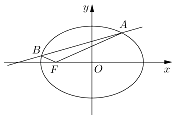
(1)求椭圆C的标准方程;
(2)对于动直线l,是否存在一个定点,无论∠OFA如何变化,直线l总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足2Sn=(an+2)bn , 其中Sn是数列{an}的前n项和.
(1)若数列{an}是首项为 ![]() ,公比为﹣
,公比为﹣ ![]() 的等比数列,求数列{bn}的通项公式;
的等比数列,求数列{bn}的通项公式;
(2)若bn=n,a2=3,求证:数列{an}满足an+an+2=2an+1 , 并写出数列{an}的通项公式;
(3)在(2)的条件下,设cn= ![]() , 求证:数列{cn}中的任意一项总可以表示成该数列其他两项之积.
, 求证:数列{cn}中的任意一项总可以表示成该数列其他两项之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},a1=a(a∈R),an+1= ![]() (n∈N*).
(n∈N*).
(1)若数列{an}从第二项起每一项都大于1,求实数a的取值范围;
(2)若a=﹣3,记Sn是数列{an}的前n项和,证明:Sn<n+ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com