
【题目】已知集合M={1,2,3,4},N={(a,b)|a∈M,b∈M},A是集合N中任意一点,O为坐标原点,则直线OA与y=x2+1有交点的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:∵集合M={1,2,3,4},N={(a,b)|a∈M,b∈M},A是集合N中任意一点,∴点A有可能是(1,2),(2,1),(1,3),(3,1),(1,4),
(4,1),(2,3),(3,2),(2,4),(4,2),(3,4),(4,3),共12种可能,
当A(1,2)时,直线OA:y=2x,与y=x2+1有交点(1,2);
当A(2,1)时,直线OA:y= ![]() x,与y=x2+1没有交点;
x,与y=x2+1没有交点;
当A(1,3)时,直线OA:y=3x,与y=x2+1有交点;
当A(3,1)时,直线OA:y= ![]() x,与y=x2+1没有交点;
x,与y=x2+1没有交点;
当A(1,4)时,直线OA:y=4x,与y=x2+1有交点;
当A(4,1)时,直线OA:y= ![]() x,与y=x2+1没有交点;
x,与y=x2+1没有交点;
当A(2,3)时,直线OA:y= ![]() x,与y=x2+1没有交点;
x,与y=x2+1没有交点;
当A(3,2)时,直线OA:y= ![]() ,与y=x2+1没有交点;
,与y=x2+1没有交点;
当A(2,4)时,直线OA:y=2x,与y=x2+1有交点(1,2);
当A(4,2)时,直线OA:y= ![]() x,与y=x2+1没有交点;
x,与y=x2+1没有交点;
当A(3,4)时,直线OA:y= ![]() x,与y=x2+1没有交点;
x,与y=x2+1没有交点;
当A(4,3)时,直线OA:y= ![]() x,与y=x2+1没有交点(1,2).
x,与y=x2+1没有交点(1,2).
∴直线OA与y=x2+1有交点的概率p= ![]() =
= ![]() .
.
故选:B.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|lgx|.若a≠b且,f(a)=f(b),则a+b的取值范围是( )
A.(1,+∞)
B.[1,+∞)
C.(2,+∞)
D.[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为3的正方体ABCD﹣A1B1C1D1中,A1E=CF=1. 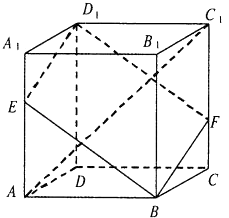
(1)求两条异面直线AC1与D1E所成角的余弦值;
(2)求直线AC1与平面BED1F所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x),g(x)分别是定义在R上的奇函数和偶函数,且f(x)+g(x)=3x .
(1)求 f(x),g(x);
(2)若对于任意实数t∈[0,1],不等式f(2t)+ag(t)<0恒成立,求实数a的取值范围;
(3)若存在m∈[﹣2,﹣1],使得不等式af(m)+g(2m)<0成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.若x在 ![]() 内,则sinx>cosx
内,则sinx>cosx
B.函数 ![]() 的图象的一条对称轴是
的图象的一条对称轴是 ![]()
C.函数 ![]() 的最大值为π
的最大值为π
D.函数y=sin2x的图象可以由函数 ![]() 的图象向右平移
的图象向右平移 ![]() 个单位而得
个单位而得
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=2sin(3x﹣ ![]() ),有下列命题:①其表达式可改写为y=2cos(3x﹣
),有下列命题:①其表达式可改写为y=2cos(3x﹣ ![]() );②y=f(x)的最小正周期为
);②y=f(x)的最小正周期为 ![]() ;③y=f(x)在区间(
;③y=f(x)在区间( ![]() ,
, ![]() )上是增函数;④将函数y=2sin3x的图象上所有点向左平行移动
)上是增函数;④将函数y=2sin3x的图象上所有点向左平行移动 ![]() 个单位长度就得到函数y=f(x)的图象.其中正确的命题的序号是(注:将你认为正确的命题序号都填上).
个单位长度就得到函数y=f(x)的图象.其中正确的命题的序号是(注:将你认为正确的命题序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(﹣1,1)上的函数f(x)满足: ![]() ,当x∈(﹣1,0)时,有f(x)>0,且
,当x∈(﹣1,0)时,有f(x)>0,且 ![]() .设
.设 ![]() ,则实数m与﹣1的大小关系为( )
,则实数m与﹣1的大小关系为( )
A.m<﹣1
B.m=﹣1
C.m>﹣1
D.不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com