
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,沿
的中点,沿![]() 将
将![]() 折起,点
折起,点![]() 折至
折至![]() 处(
处(![]() 与
与![]() 不重合),若
不重合),若![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,则在
的中点,则在![]() 折起过程中( )
折起过程中( )
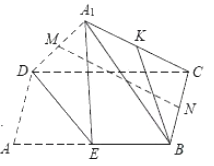
A.![]() 可以与
可以与![]() 垂直
垂直
B.不能同时做到![]() 平面
平面![]() 且
且![]() 平面
平面![]()
C.当![]() 时,
时,![]() 平面
平面![]()
D.直线![]() 、
、![]() 与平面
与平面![]() 所成角分别为
所成角分别为![]() 、
、![]() ,
,![]() 、
、![]() 能够同时取得最大值
能够同时取得最大值
【答案】D
【解析】
逐一分析各选项的正误,从而可得出结论.
对于A,连接![]() ,假设
,假设![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
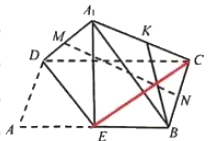
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
而![]() ,
,![]() A错误;
A错误;
对于B,取![]() 、
、![]() 中点
中点![]() 、
、![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,
,
则![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
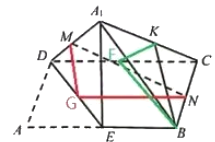
![]() ,
,![]() ,则四边形
,则四边形![]() 为梯形,且
为梯形,且![]() 、
、![]() 为底,
为底,
又![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,同理可得
,同理可得![]() 平面
平面![]() ,B选项错误;
,B选项错误;
对于C,连接![]() 、
、![]() ,
,
当![]() 时,
时,![]() ,
,
而![]() ,
,![]() ,
,
![]() 与
与![]() 不垂直,即
不垂直,即![]() 不垂直平面
不垂直平面![]() ,C选项错误;
,C选项错误;
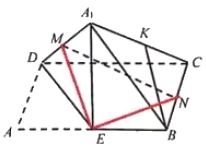
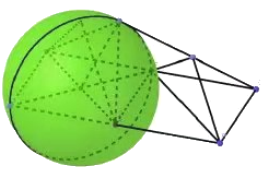
对于D,![]() 在以
在以![]() 为直径球面上,球心为
为直径球面上,球心为![]() ,
,
![]() 的轨迹为
的轨迹为![]() 外接圆(
外接圆(![]() 与
与![]() 不重合,
不重合,![]() 为
为![]() 的中点),
的中点),
连接![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,则
,则![]() ,
,![]() ,
,
且![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
由余弦定理得![]() ,
,![]() .
.
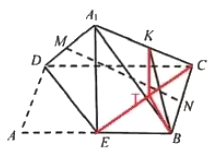
当直线![]() 与平面
与平面![]() 所成角取得最大值时,点
所成角取得最大值时,点![]() 到平面
到平面![]() 的距离最大,
的距离最大,
由于点![]() 为
为![]() 的中点,此时,点
的中点,此时,点![]() 到平面
到平面![]() 的距离最大,
的距离最大,
由于![]() ,当
,当![]() 与平面
与平面![]() 所成角最大时,点
所成角最大时,点![]() 到平面
到平面![]() 的距离最大.
的距离最大.
所以,直线![]() 、
、![]() 与平面
与平面![]() 所成角能同时取到最大值.
所成角能同时取到最大值.
故选:D.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】上饶市在某次高三适应性考试中对数学成绩数据统计显示,全市10000名学生的成绩近似服从正态分布![]() ,现某校随机抽取了50名学生的数学成绩分析,结果这50名学生的成绩全部介于85分到145分之间,现将结果按如下方式分为6组,第一组
,现某校随机抽取了50名学生的数学成绩分析,结果这50名学生的成绩全部介于85分到145分之间,现将结果按如下方式分为6组,第一组![]() ,第二组
,第二组![]() ,…,第六组
,…,第六组![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
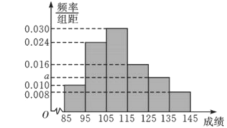
(1)试由样本频率分布直方图估计该校数学成绩的平均分数;
(2)若从这50名学生中成绩在125分(含125分)以上的同学中任意抽取3人,该3人在全市前13名的人数记为![]() ,求
,求![]() 的概率.
的概率.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型工厂招聘到一大批新员工.为了解员工对工作的熟练程度,从中随机抽取100人组成样本,统计他们每天加工的零件数,得到如下数据:

将频率作为概率,解答下列问题:
(1)当![]() 时,从全体新员工中抽取2名,求其中恰有1名日加工零件数达到240及以上的概率;
时,从全体新员工中抽取2名,求其中恰有1名日加工零件数达到240及以上的概率;
(2)若根据上表得到以下频率分布直方图,估计全体新员工每天加工零件数的平均数为222个,求![]() 的值(每组数据以中点值代替);
的值(每组数据以中点值代替);
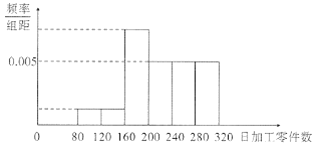
(3)在(2)的条件下,工厂按工作熟练度将新员工分为三个等级:日加工零件数未达200的员工为C级;达到200但未达280的员工为B级;其他员工为A级.工厂打算将样本中的员工编入三个培训班进行全员培训:A,B,C三个等级的员工分别参加高级、中级、初级培训班,预计培训后高级、中级、初级培训班的员工每人的日加工零件数分别可以增加20,30,50.现从样本中随机抽取1人,其培训后日加工零件数增加量为X,求随机变量X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解高中生的艺术素养,从学校随机选取男,女同学各50人进行研究,对这100名学生在音乐、美术、戏剧、舞蹈等多个艺术项目进行多方位的素质测评,并把调查结果转化为个人的素养指标![]() 和
和![]() ,制成下图,其中“*”表示男同学,“+”表示女同学.
,制成下图,其中“*”表示男同学,“+”表示女同学.

若![]() ,则认定该同学为“初级水平”,若
,则认定该同学为“初级水平”,若![]() ,则认定该同学为“中级水平”,若
,则认定该同学为“中级水平”,若![]() ,则认定该同学为“高级水平”;若
,则认定该同学为“高级水平”;若![]() ,则认定该同学为“具备一定艺术发展潜质”,否则为“不具备明显艺术发展潜质”.
,则认定该同学为“具备一定艺术发展潜质”,否则为“不具备明显艺术发展潜质”.
(I)从50名女同学的中随机选出一名,求该同学为“初级水平”的概率;
(Ⅱ)从男同学所有“不具备明显艺术发展潜质的中级或高级水平”中任选2名,求选出的2名均为“高级水平”的概率;
(Ⅲ)试比较这100名同学中,男、女生指标![]() 的方差的大小(只需写出结论).
的方差的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代十进制的算筹计数法,在世界数学史上是一个伟大的创造. 算筹实际上是一根根同样长短的小木棍,用算筹表示数1~9的方法如图:例如:163可表示为“![]() ”,27可表示为“
”,27可表示为“![]() ”.现有6根算筹,用来表示不能被10整除的两位数,算筹必须用完,则这样的两位数的个数为_________.
”.现有6根算筹,用来表示不能被10整除的两位数,算筹必须用完,则这样的两位数的个数为_________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 正方形
正方形![]() 所在平面,M是
所在平面,M是![]() 的中点,二面角
的中点,二面角![]() 的大小为
的大小为![]() .
.

(1)设l是平面![]() 与平面
与平面![]() 的交线,证明
的交线,证明![]() ;
;
(2)在棱![]() 是否存在一点N,使
是否存在一点N,使![]() 为
为![]() 的二面角.若不存在,说明理由:若存在,求
的二面角.若不存在,说明理由:若存在,求![]() 长.
长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com