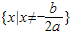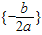设一元二次方程Ax2+Bx+C=0,根据下列条件分别求解.
(1)若A=1,B、C是一枚骰子先后掷两次出现的点数,求方程有实数根的概率;
(2)设B=-A,C=A-3,A随机的取实数使方程有实数根,求方程至少有一个非负实数根的概率.
【答案】
分析:(1)由题意知本题是一个古典概型,试验发生所包含的事件数36,满足条件的事件是当A=1时Ax
2+Bx+C=0,变为x
2+Bx+C=0方程有实数解得B
2-4C≥0 显然B≠1,列举出所有的事件,得到概率.
(2)由题意知本题是一个几何概型,试验发生包含的事件是A随机的取实数使方程有实数根,根据一元二次方程判别式得到A的范围,满足条件的事件是使得方程有至少有一个非负实数根,根据对立事件的概率得到结果.
解答:解:(1)由题意知本题是一个古典概型,
当A=1时Ax
2+Bx+C=0,变为x
2+Bx+C=0
方程有实数解得B
2-4C≥0 显然B≠1
若B=2时C=1;1种
若B=3时C=1,2;2种
若B=4时C=1,2,3,4;4种
若B=5时C=1,2,3,4,5,6;6种
若B=6时C=1,2,3,4,5,6;6种故有19种,
方程有实数根的概率是
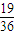
(2)B=-A,C=A-3,且方程有实数根,得
A≠0,△=A
2-4A(A-3)≥0,得0<A≤4
而方程有两个正数根的条件是:A≠0,△=A
2-4A(A-3)≥0
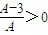
即3<A≤4
故方程有两个正数根的概率是
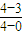
=

而方程至少有一个非负实数根的对立事件是方程有两个正数根故所求的概率为1-

=
 点评:
点评:本题考查等可能事件的概率,一元二次方程实根分布,是一个综合题,解题的关键是对于一元二次方程的解的情况的分析,解题时有一定难度.

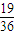
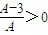
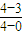 =
=
 =
=


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案