
【题目】设函数f(x)![]() (m∈R).
(m∈R).
(1)当m=1时,求函数的单调区间;
(2)若函数F(x)=f(x)+x![]() m+2有两个零点,求实数m的取值范围.
m+2有两个零点,求实数m的取值范围.
【答案】(1) 递增区间为(0,e),递减区间为(e,+∞) (2) (﹣∞,﹣2e).
【解析】
(1)![]() 时,求出
时,求出![]() ,求出
,求出![]() 的解,即可得出结论;
的解,即可得出结论;
(2)求出![]() 整理,
整理,![]() 有两个零点,转化为函数
有两个零点,转化为函数![]() 有两个零点,求
有两个零点,求![]() ,求出极值点
,求出极值点![]() ,分析函数值的变化趋势,只需g(x)的极小值g(
,分析函数值的变化趋势,只需g(x)的极小值g(![]() )<0方程有两个零点,解不等式g(
)<0方程有两个零点,解不等式g(![]() )<0,即可求出结论.
)<0,即可求出结论.
(1)当m=1时,f(x)![]() ,x>0,∴f'(x)
,x>0,∴f'(x)![]() ,
,
令f'(x)=0,得1﹣lnx=0,x=e,
随![]() 的变化
的变化![]() 变化如下表:
变化如下表:
x | (0,e) | e | (e,+∞) |
f'(x) | + | 0 | ﹣ |
f(x) | 递增 | 极大值 | 递减 |
∴函数f(x)的单调递增区间为(0,e),单调递减区间为(e,+∞);
(2)F(x)![]() x
x![]() m+2,定义域为(0,+∞),
m+2,定义域为(0,+∞),
∴F(x)![]() x
x![]() m+2
m+2![]() ,
,
设g(x)=4mlnx+4x2+m2+4mx+8x,
∵函数F(x)=f(x)+x![]() m+2有两个零点,
m+2有两个零点,
∴函数g(x)=4mlnx+4x2+m2+4mx+8x有两个零点,
∵g'(x)![]() ,
,
令g'(x)=0得,x![]() ,
,
∵函数g(x)=4mlnx+4x2+m2+4mx+8x有两个零点,
∴函数g(x)在(0,+∞)上不单调,∴![]() 0,∴m<0,
0,∴m<0,
随![]() 的变化
的变化![]() 变化如下表:
变化如下表:
x | (0, |
| ( |
g'(x) | ﹣ | 0 | + |
g(x) | 递减 | 极小值 | 递增 |
∴函数g(x)的极小值为g(![]() ),
),
∵当x→0时,g(x)→+∞;当x→+∞时,g(x)→+∞,
∴若函数g(x)=4mlnx+4x2+m2+4mx+8x有两个零点,
则函数g(x)的极小值g(![]() )<0,
)<0,
即4mln(![]() )+4
)+4![]() m2﹣4m
m2﹣4m![]() 4m<0,
4m<0,
∴mln(![]() )﹣m<0,又∵m<0,∴ln(
)﹣m<0,又∵m<0,∴ln(![]() )>1,
)>1,
∴![]() e,∴m<﹣2e,
e,∴m<﹣2e,
∴实数m的取值范围为:(﹣∞,﹣2e).


科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 上有最大值4,最小值1,设函数
上有最大值4,最小值1,设函数![]() .
.
(1)求![]() 、
、![]() 的值及函数
的值及函数![]() 的解析式;
的解析式;
(2)若不等式![]() 在
在![]() 时恒成立,求实数
时恒成立,求实数![]() 的取值范围;
的取值范围;
(3)如果关于![]() 的方程
的方程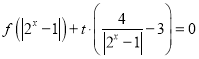 有三个相异的实数根,求实数
有三个相异的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 是双曲线
是双曲线![]() 的一条渐近线,点
的一条渐近线,点![]() 在双曲线C上,设坐标原点为O.
在双曲线C上,设坐标原点为O.
(1)求双曲线C的方程;
(2)若过点![]() 的直线l与双曲线C交于R、S两点,若
的直线l与双曲线C交于R、S两点,若![]() ,求直线l的方程;
,求直线l的方程;
(3)设![]() 在双曲线上,且直线AM与y轴相交于点P,点M关于y轴对称的点为N,直线AN与y轴相交于点Q,问:在x轴上是否存在定点T,使得
在双曲线上,且直线AM与y轴相交于点P,点M关于y轴对称的点为N,直线AN与y轴相交于点Q,问:在x轴上是否存在定点T,使得![]() ?若存在,求出点T的坐标;若不存在,说明理由.
?若存在,求出点T的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为![]() 的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.

(1)若围墙AP,AQ总长度为200米,如何围可使得三角形地块APQ的面积最大?
(2)已知AP段围墙高1米,AQ段围墙高1.5米,造价均为每平方米100元.若围围墙用了20000元,问如何围可使竹篱笆用料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,若对任意正整数n,总存在正整数m,使得
,若对任意正整数n,总存在正整数m,使得![]() ,则称
,则称![]() 是“H数列”;
是“H数列”;
(1)若数列![]() 的前n项和
的前n项和![]() (
(![]() ),判断数列
),判断数列![]() 是否是“H数列”?若是,给出证明;若不是,说明理由;
是否是“H数列”?若是,给出证明;若不是,说明理由;
(2)设数列![]() 是常数列,证明:
是常数列,证明:![]() 为“H数列”的充要条件是
为“H数列”的充要条件是![]() ;
;
(3)设![]() 是等差数列,其首项
是等差数列,其首项![]() ,公差
,公差![]() ,若
,若![]() 是“H数列”,求d的值;
是“H数列”,求d的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(数学文卷·2017届重庆十一中高三12月月考第16题) 现介绍祖暅原理求球体体积公式的做法:可构造一个底面半径和高都与球半径相等的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,用这样一个几何体与半球应用祖暅原理(图1),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为![]() ,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
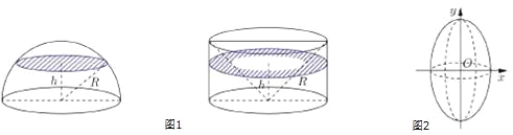
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知曲线![]() 的方程为
的方程为![]() ,曲线
,曲线![]() 的方程为
的方程为![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴正半轴建立直角坐标系
轴正半轴建立直角坐标系![]() .
.
(1)求曲线![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与曲线
,与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 、
、![]() 是两个垃圾中转站,
是两个垃圾中转站,![]() 在
在![]() 的正东方向
的正东方向![]() 千米处,
千米处,![]() 的南面为居民生活区.为了妥善处理生活垃圾,政府决定在
的南面为居民生活区.为了妥善处理生活垃圾,政府决定在![]() 的北面建一个垃圾发电厂
的北面建一个垃圾发电厂![]() .垃圾发电厂
.垃圾发电厂![]() 的选址拟满足以下两个要求(
的选址拟满足以下两个要求(![]() 、
、![]() 、
、![]() 可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点
可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点![]() 到直线
到直线![]() 的距离要尽可能大).现估测得
的距离要尽可能大).现估测得![]() 、
、![]() 两个中转站每天集中的生活垃圾量分别约为
两个中转站每天集中的生活垃圾量分别约为![]() 吨和
吨和![]() 吨.设
吨.设![]() .
.
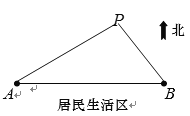
(1)求![]() (用
(用![]() 的表达式表示);
的表达式表示);
(2)垃圾发电厂该如何选址才能同时满足上述要求?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com