
【题目】如图所示,在矩形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使二面角
的位置,使二面角![]() 是直二面角.
是直二面角.

(1)证明: ![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】某厂以![]() 千克/小时的速度匀速生产某种产品(生产条件要求
千克/小时的速度匀速生产某种产品(生产条件要求![]() ),每一小时可获得的利润是
),每一小时可获得的利润是![]() 元.
元.
(1)要使生产该产品2小时获得的利润不低于1500元,求![]() 的取值范围;
的取值范围;
(2) 要使生产480千克该产品获得的利润最大,问:该厂应该选取何种生产速度?并求此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 、
、![]() 分别为左、右顶点,
分别为左、右顶点,![]() 为其右焦点,
为其右焦点,![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 、
、![]() 的动点,且
的动点,且![]() 的最小值为-2.
的最小值为-2.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过左焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的损坏,可见部分如下:

试着根据表中的信息解答下列问题:
(Ⅰ)求全班的学生人数及分数在[70,80)之间的频数;
(Ⅱ)为快速了解学生的答题情况,老师按分层抽样的方法从位于[70,80)和[80,90)分数段的试卷中抽取7份进行分析,再从中任选2人进行交流,求交流的学生中,成绩位于[70,80)分数的人恰有一人被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】英州育才中学某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分別到气象局与市医院抄录了![]() 至
至![]() 月份每月
月份每月![]() 号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料(表):
号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料(表):
日期 |
|
|
|
|
|
|
昼夜温差 |
|
|
|
|
|
|
就诊人数 |
|
|
|
|
|
|
该兴趣小组确定的研究方案是:先从这六组数据中选取![]() 组,用剩下的
组,用剩下的![]() 组数据求线性回归方程,再用被选取的
组数据求线性回归方程,再用被选取的![]() 组数据进行检验.
组数据进行检验.
(1)求选取的![]() 组数据恰好是相邻两个月的概率;
组数据恰好是相邻两个月的概率;
(2)求选取的是![]() 月与
月与![]() 月的两组数据,请根据
月的两组数据,请根据![]() 至
至![]() 月份的数据,求出
月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
其中回归系数公式, ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.对收回的100份有效问卷进行统计,得到如![]() 下列联表:
下列联表:
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现按女生是否能做到科学用眼进行分层,从45份女生问卷中抽取了6份问卷,从这6份问卷中再随机抽取3份,并记其中能做到科学用眼的问卷的份数![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过![]() 的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的
的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量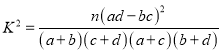 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】衡阳市为增强市民的环境保护意识,面向全市征召义务宣传志愿者,现从符合条件的志愿者中随机抽取100名后按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,则应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该市决定在第3,4组的志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在10名学生中,男生有x名,现从10名学生中任选6人去参加某项活动:①至少有1名女生;②5名男生,1名女生;③3名男生,3名女生.若要使①为必然事件,②为不可能事件,③为随机事件,则x=( )
A.5B.6C.3或4D.5或6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com