
分析 由$\frac{y-3}{x-4}$的几何意义为$\frac{{x}^{2}}{4}$+y2=1(y≥0)上的动点与定点M(4,3)连线的斜率,借助于两点求斜率可得$\frac{y-3}{x-4}$的最大值,再设出过点M(4,3)的直线方程,联立直线方程和椭圆方程,化为关于x的一元二次方程,由判别式等于0求得$\frac{y-3}{x-4}$的最小值.
解答 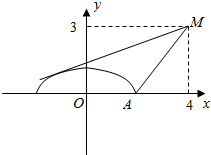 解:如图,$\frac{y-3}{x-4}$的几何意义为$\frac{{x}^{2}}{4}$+y2=1(y≥0)上的动点与定点M(4,3)连线的斜率,
解:如图,$\frac{y-3}{x-4}$的几何意义为$\frac{{x}^{2}}{4}$+y2=1(y≥0)上的动点与定点M(4,3)连线的斜率,
∵${k}_{MA}=\frac{3-0}{4-2}=\frac{3}{2}$,∴$\frac{y-3}{x-4}$的最大值为$\frac{3}{2}$;
设过M(4,3)的直线方程为y-3=k(x-4),即y=kx-4k+3,
联立$\left\{\begin{array}{l}{y=kx-4k+3}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,得(1+4k2)x2-(32k2-24k)x+64k2-96k+32=0.
由△=(32k2-24k)2-(4+16k2)(64k2-96k+32)=0,
整理得:3k2-6k+2=0,解得k=$\frac{3-\sqrt{3}}{3}$或k=$\frac{3+\sqrt{3}}{3}$(舍),
∴$\frac{y-3}{x-4}$的最小值为$\frac{3-\sqrt{3}}{3}$.
故答案为:$[\frac{3-\sqrt{3}}{3},\frac{3}{2}]$.
点评 本题考查椭圆的简单性质,考查了数形结合的解题思想方法,该题也可利用三角代换求解,是中档题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | [15,+∞) | B. | (-∞,19] | C. | (15,19) | D. | [15,19] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在△OAB中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,点M是AB的靠近B的一个三等分点,点N是OA的靠近A的一个四等分点,若OM与BN相交于点P,求$\overrightarrow{OP}$.
如图所示,在△OAB中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,点M是AB的靠近B的一个三等分点,点N是OA的靠近A的一个四等分点,若OM与BN相交于点P,求$\overrightarrow{OP}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{2}{e}$] | B. | (-∞,$\frac{2}{e}$) | C. | (-∞,0] | D. | (-∞,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com