
【题目】已知二次函数f(x)=x2+bx+c(b,c∈R)
(1)若f(x)的图象与x轴有且仅有一个交点,求b2+c2+2的取值范围;
(2)在b≥0的条件下,若f(x)的定义域[﹣1,0],值域也是[﹣1,0],符合上述要求的函数f(x)是否存在?若存在,求出f(x)的表达式,若不存在,请说明理由.
【答案】
(1)解:由于f(x)的图象与x轴有且仅有一个交点,故△=0,
即△=b2﹣4c=0b2=4c,
则b2+c2+2=c2+4c+2=(c+2)2﹣4≥﹣4;
(2)解:设符合条件的f(x)存在,
∵函数图象的对称轴是x=﹣ ![]() ,
,
又b≥0,∴﹣ ![]() ≤0.
≤0.
①当﹣ ![]() <﹣
<﹣ ![]() ≤0,即0≤b<1时,
≤0,即0≤b<1时,
函数x=﹣ ![]() 有最小值﹣1,则
有最小值﹣1,则 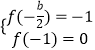
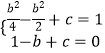
![]() 或
或 ![]() (舍去).
(舍去).
②当﹣1<﹣ ![]() ≤﹣
≤﹣ ![]() ,即1≤b<2时,则
,即1≤b<2时,则 
![]() (舍去)或
(舍去)或 ![]() (舍去).
(舍去).
③当﹣ ![]() ≤﹣1,即b≥2时,函数在[﹣1,0]上单调递增,则
≤﹣1,即b≥2时,函数在[﹣1,0]上单调递增,则 ![]() ,解得
,解得 ![]() ,
,
综上所述,符合条件的函数有两个,
f(x)=x2﹣1或f(x)=x2+2x
【解析】(1)根据二次函数的性质得到判别式△=0,求出b2=4c,代入b2+c2+2,求出其范围即可;(2)二次函数f(x)=x2+bx+c(b≥0,c∈R)的对称轴是x=﹣ ![]() ,定义域为[﹣1,0],按照对称轴在定义域[﹣1,0]内、在[﹣1,0]的左边和在[﹣1,0]的右边三种情况分别求函数的值域,令其和题目条件中给出的值域相等,求b和c.
,定义域为[﹣1,0],按照对称轴在定义域[﹣1,0]内、在[﹣1,0]的左边和在[﹣1,0]的右边三种情况分别求函数的值域,令其和题目条件中给出的值域相等,求b和c.
【考点精析】掌握二次函数的性质是解答本题的根本,需要知道当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】某厂家拟在2017年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() (单位:万件)与年促销费用
(单位:万件)与年促销费用![]() (单位:万元)(
(单位:万元)(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2017年该产品的利润![]() (单位:万元)表示为年促销费用
(单位:万元)表示为年促销费用![]() (单位:万元)的函数;
(单位:万元)的函数;
(2)该厂家2017年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣1,g(x)=﹣x2+4x﹣3,若有f(a)=g(b),则b的取值范围为( )
A.![]()
B.(2﹣ ![]() ,2+
,2+ ![]() )
)
C.[1,3]
D.(1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,过点
,过点![]() 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,
, ![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,连接
两点,连接![]() (
(![]() 为坐标原点)并延长交椭圆
为坐标原点)并延长交椭圆![]() 于点
于点![]() ,求
,求![]() 面积的最大值及取最大值时直线
面积的最大值及取最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年11月,第十一届中国(珠海)国际航空航天博览会开幕式当天,歼-20的首次亮相给观众留下了极深的印象.某参赛国展示了最新研制的两种型号的无人机,先从参观人员中随机抽取100人对这两种型号的无人机进行评价,评价分为三个等级:优秀、良好、合格.由统计信息可知,甲型号无人机被评为优秀的频率为![]() 、良好的频率为
、良好的频率为![]() ;乙型号无人机被评为优秀的频率为
;乙型号无人机被评为优秀的频率为![]() ,且被评为良好的频率是合格的频率的5倍.
,且被评为良好的频率是合格的频率的5倍.
(1) 求这100人中对乙型号无人机评为优秀和良好的人数;
(2) 如果从这100人中按对甲型号无人机的评价等级用分层抽样的方法抽取5人,然后从其他对乙型号无人机评优秀、良好的人员中各选取1人进行座谈会,会后从这7人中随机抽取2人进行现场操作体验活动,求进行现场操作体验活动的2人都评优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 内,动点
内,动点![]() 与两定点
与两定点![]() ,
, ![]() 连线的斜率之积为
连线的斜率之积为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设点![]() ,
, ![]() 是轨迹
是轨迹![]() 上相异的两点.
上相异的两点.
(Ⅰ)过点![]() ,
, ![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() ,
, ![]() ,
, ![]() 与
与![]() 两条切线相交于点
两条切线相交于点![]() ,证明:
,证明: ![]() ;
;
(Ⅱ)若直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,证明:
,证明: ![]() 为定值,并求出这个定值.
为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间共有![]() 名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.

(Ⅰ) 根据茎叶图计算样本均值;
(Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间![]() 名工人中有几名优秀工人;
名工人中有几名优秀工人;
(Ⅲ) 从该车间![]() 名工人中,任取2人,求恰有1名优秀工人的概率.
名工人中,任取2人,求恰有1名优秀工人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com