
【题目】某种蔬菜从1月1日起开始上市,通过市场调查,得到该蔬菜种植成本![]() (单位:元/
(单位:元/![]() )与上市时间
)与上市时间![]() (单位:10天)的数据如下表:
(单位:10天)的数据如下表:
时间 | 5 | 11 | 25 |
种植成本 | 15 | 10.8 | 15 |
(1)根据上表数据,从下列函数:![]() ,
,![]() ,
,![]() ,
,![]() 中(其中
中(其中![]() ),选取一个合适的函数模型描述该蔬菜种植成本
),选取一个合适的函数模型描述该蔬菜种植成本![]() 与上市时间
与上市时间![]() 的变化关系;
的变化关系;
(2)利用你选取的函数模型,求该蔬菜种植成本最低时的上市时间及最低种植成本.
【答案】(1)![]() ;(2)该蔬菜上市150天时,该蔬菜种植成本最低为10(元/
;(2)该蔬菜上市150天时,该蔬菜种植成本最低为10(元/![]() ).
).
【解析】
(1)先作出散点图,根据散点图的分布即可判断只有模型![]() 符合,然后将数据代入建立方程组,求出参数
符合,然后将数据代入建立方程组,求出参数![]() .
.
(2)由于模型为二次函数,结合定义域,利用配方法即可求出最低种植成本以及对应得上市时间.
解:(1)以上市时间![]() (单位:10天)为横坐标,以种植成本
(单位:10天)为横坐标,以种植成本![]() (单位/
(单位/![]() )为纵坐标,画出散点图(如图).
)为纵坐标,画出散点图(如图).
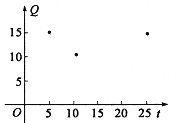
根据点的分布特征,![]() ,
,![]() ,
,![]() 这三个函数模型与表格所提供的数据不吻合,只有函数模型与表格所提供的数据吻合最好,
这三个函数模型与表格所提供的数据不吻合,只有函数模型与表格所提供的数据吻合最好,
所以选取函数模型![]() 进行描述该蔬菜种植成本
进行描述该蔬菜种植成本![]() 与上市时间
与上市时间![]() 的变化关系.
的变化关系.
将表格所提供的三组数据分别代入![]() ,
,
得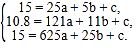
解得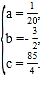
所以,描述该蔬菜种植成本![]() 与上市时间
与上市时间![]() 的变化关系的函数为
的变化关系的函数为![]() .
.
(2)由(1)知![]() ,
,
所以当![]() 时,
时,![]() 的最小值为10,
的最小值为10,
即该蔬菜上市150天时,该蔬菜种植成本最低为10(元/![]() ).
).


科目:高中数学 来源: 题型:
【题目】某市每年春节前后,由于大量的烟花炮竹的燃放,空气污染较为严重.该市环保研究所对近年春节前后每天的空气污染情况调查研究后发现,每天空气污染的指数.f(t),随时刻t(时)变化的规律满足表达式![]() ,其中a为空气治理调节参数,且a∈(0,1).
,其中a为空气治理调节参数,且a∈(0,1).
(1)令![]() ,求x的取值范围;
,求x的取值范围;
(2)若规定每天中f(t)的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过5,试求调节参数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点
的中点
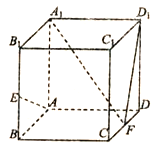
(1)求证:![]() 面
面![]() ;
;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 面
面![]() ,若存在,试确定
,若存在,试确定![]() 的值,若不存在说明理由;
的值,若不存在说明理由;
(3)在(2)的条件下,求面![]() 与面
与面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:

记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元), ![]() 表示购机的同时购买的易损零件数.
表示购机的同时购买的易损零件数.
(Ⅰ)若![]() =19,求y与x的函数解析式;
=19,求y与x的函数解析式;
(Ⅱ)若要求“需更换的易损零件数不大于![]() ”的频率不小于0.5,求
”的频率不小于0.5,求![]() 的最小值;
的最小值;
(Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com