
(1)建立适当的坐标系,求椭圆的方程;
(2)设椭圆C上有两点P、Q使∠PMQ的平分线垂直于AO,证明:存在实数λ,使PQ=λAB.
答案:(1)以O为原点,以射线OA为x轴的正向,建立如图所示的坐标系,则A(2,0).
于是可设C:=![]() =1.
=1.
∵![]() =0,∴AM⊥BM
=0,∴AM⊥BM![]() cos∠ABM=
cos∠ABM=![]() .
.
从而,![]() =|BM|·|BA|·
=|BM|·|BA|·![]() =|BM|2=8
=|BM|2=8![]() |BM|=
|BM|=![]() .
.
由对称性知,|MO|=![]() |BM|=
|BM|=![]() .
.
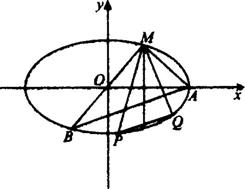
第22题图
∴M(1,1),B(-1,-1).
代入C的方程,得![]() =1
=1![]() b2=
b2=![]() .
.
故C:![]() =1.
=1.
(2)∵∠PMQ的平分线垂直于x轴,∴可设直线MP的斜率为k,MQ的斜率为-k.
于是MP:y-1=k(x-1),MQ:y-1=-k(k-1).
从MP与C的方程中消去y,得
(1+3k2)x2-6k(k-1)x+3k2-6k-1=0.
设P(x1,y1),Q(x2,y2).
由于M(1,1)在C上,∴x1=x1·1=![]()
同理可得x2=![]() .
.
∵y1=k(x1-1)+1,y2=-k(x2-1)+1.
∴kPQ=![]() =
= .
.
又kAB=![]() ,从而
,从而![]() .故存在实数λ,使
.故存在实数λ,使![]() .
.


科目:高中数学 来源: 题型:
| 3 |
| PE |
| QE |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com