
【题目】我校甲、乙、丙三名语文老师和![]() 、
、![]() 、
、![]() 三名数学老师被派往某县城一中和二中支教,其中有一名语文老师和一名数学老师被派到了一中,其它老师都去二中支教,则甲与
三名数学老师被派往某县城一中和二中支教,其中有一名语文老师和一名数学老师被派到了一中,其它老师都去二中支教,则甲与![]() 被派到同一所学校的概率为( )
被派到同一所学校的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】哈尔滨市第三中学校响应教育部门疫情期间“停课不停学”的号召,实施网络授课,为检验学生上网课的效果,高三学年进行了一次网络模拟考试.全学年共![]() 人,现从中抽取了
人,现从中抽取了![]() 人的数学成绩,绘制成频率分布直方图(如下图所示).已知这
人的数学成绩,绘制成频率分布直方图(如下图所示).已知这![]() 人中
人中![]() 分数段的人数比
分数段的人数比![]() 分数段的人数多
分数段的人数多![]() 人.
人.
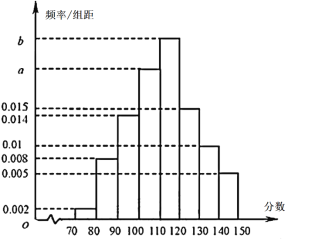
(1)根据频率分布直方图,求![]() 、
、![]() 的值,并估计抽取的
的值,并估计抽取的![]() 名同学数学成绩的中位数;
名同学数学成绩的中位数;
(2)若学年打算给数学成绩不低于![]() 分的同学颁发“网络课堂学习优秀奖”,将这
分的同学颁发“网络课堂学习优秀奖”,将这![]() 名同学数学成绩的样本频率视为概率.
名同学数学成绩的样本频率视为概率.
(i)估计全学年的获奖人数;
(ii)若从全学年随机选取![]() 人,求所选
人,求所选![]() 人中至少有
人中至少有![]() 人获奖的概率.
人获奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900
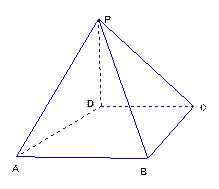
(1)求证:PC⊥BC
(2)求点A到平面PBC的距离
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a=2![]() ,_______,求△ABC的周长l的范围.
,_______,求△ABC的周长l的范围.
在①![]() (﹣cos
(﹣cos![]() ,sin
,sin![]() ),
),![]() (cos
(cos![]() ,sin
,sin![]() ),且
),且![]()
![]() ,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x
,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x![]() )
)![]() ,f(A)
,f(A)![]()
注:这三个条件中任选一个,补充在上面问题中并对其进行求解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABCD中,![]() ,_________,DC=2,在下面给出的三个条件中任选一个,补充在上面的问题中,并加以解答.(选出一种可行的方案解答,若选出多个方案分别解答,则按第一个解答记分)①
,_________,DC=2,在下面给出的三个条件中任选一个,补充在上面的问题中,并加以解答.(选出一种可行的方案解答,若选出多个方案分别解答,则按第一个解答记分)①![]() ;②
;②![]() ;③
;③![]() .
.
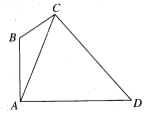
(1)求![]() 的大小;
的大小;
(2)求△ADC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=lnx,g(x)=ex.
(1)若函数φ (x) = f (x)-![]() ,求函数φ (x)的单调增区间;
,求函数φ (x)的单调增区间;
(2)设直线l为函数的图象上一点A(x0,f (x0))处的切线.证明:在区间(1,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com