
【题目】(题文)(题文)已知椭圆![]() 的离心率为
的离心率为![]() ,过右焦点
,过右焦点![]() 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆![]() 于A,B两点, N为弦AB的中点,O为坐标原点.
于A,B两点, N为弦AB的中点,O为坐标原点.
(1)求直线ON的斜率![]() ;
;
(2)求证:对于椭圆![]() 上的任意一点M,都存在
上的任意一点M,都存在![]() ,使得
,使得![]() 成立.
成立.
【答案】(1) ![]() .
.
(2)见解析.
【解析】分析:(1)设椭圆的焦距为![]() ,由
,由![]() ,可得
,可得![]() ,从而椭圆
,从而椭圆![]() 的方程可化为
的方程可化为![]() ,右焦点
,右焦点![]() ,直线
,直线![]() 所在的直线方程为
所在的直线方程为![]() ,与椭圆方程联立化为
,与椭圆方程联立化为![]() ,在利用中点公式与斜率公式即可求出;
,在利用中点公式与斜率公式即可求出;
(2)利用平面向量的基本定理,根与系数的关系,点与椭圆的位置关系,即可得到证明.
详解: (1)设椭圆的焦距为![]() ,因为
,因为![]() ,所以有
,所以有![]() ,故有
,故有![]() .
.
从而椭圆![]() 的方程可化为:
的方程可化为:![]()
知右焦点![]() 的坐标为(
的坐标为(![]() ),据题意有
),据题意有![]() 所在的直线方程为:
所在的直线方程为:![]() . ②由①,②有:
. ②由①,②有:![]() .
.
③设![]() ,弦
,弦![]() 的中点
的中点![]() ,由③及韦达定理有:
,由③及韦达定理有:
![]()
所以![]() ,即为所求.
,即为所求.
(2)显然![]() 与
与![]() 可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量
可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量![]() ,有且只有一对实数
,有且只有一对实数![]() ,使得等式
,使得等式![]() 成立.设
成立.设![]() ,由(1)中各点的坐标有:
,由(1)中各点的坐标有:![]() ,故
,故![]() .
.
又因为点![]() 在椭圆
在椭圆![]() 上,所以有
上,所以有![]() 整理可得:
整理可得:
![]() . ④
. ④
由③有:![]() .所以
.所以
![]() ⑤又点
⑤又点![]() 在椭圆
在椭圆![]() 上,故有
上,故有![]() .
.
⑥将⑤,⑥代入④可得:![]() .
.
所以,对于椭圆上的每一个点![]() ,总存在一对实数,使等式
,总存在一对实数,使等式![]() 成立,且
成立,且![]() .
.
所以存在![]() ,使得
,使得![]() .也就是:对于椭圆
.也就是:对于椭圆![]() 上任意一点
上任意一点![]() ,总存在
,总存在![]() ,使得等式
,使得等式![]() 成立.
成立.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】从你所在班级任意选出6名同学,调查他们的出生月份,假设出生在一月,二月……十二月是等可能的.设事件![]() “至少有两人出生月份相同”,设计一种试验方法,模拟20次,估计事件
“至少有两人出生月份相同”,设计一种试验方法,模拟20次,估计事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆C过定点F(2,0),且与直线x=-2相切,圆心C的轨迹为E,
(1)求圆心C的轨迹E的方程;
(2)若直线l交E与P,Q两点,且线段PQ的中心点坐标(1,1),求|PQ|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为一个摩天轮示意图。该摩天轮圆半径为4.8m,圆上最低点与地面距离为0.8m,60s转动一周.图中OA与地面垂直。以O为始边,逆时针转动0角到OB设B点与地面的距离为hm.

(1)求h与![]() 的函数解析式;
的函数解析式;
(2)设从OA开始转动,经过ts到达OB,求h与t的函数解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若f (x)在区间(-∞,2)上为单调递增函数,求实数a的取值范围;
(2)若a=0,x0<1,设直线y=g(x)为函数f (x)的图象在x=x0处的切线,求证:f (x)≤g(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,没售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损0.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了130吨该商品,现以![]() (单位:吨,
(单位:吨,![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量,![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
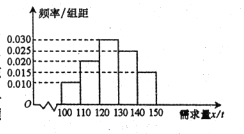
(Ⅰ)视![]() 分布在各区间内的频率为相应的概率,求
分布在各区间内的频率为相应的概率,求![]() ;
;
(Ⅱ)将![]() 表示为
表示为![]() 的函数,求出该函数表达式;
的函数,求出该函数表达式;
(Ⅲ)在频率分布直方图的市场需求量分组中,以各组的区间中点值(组中值)代表该组的各个值,并以市场需求量落入该区间的频率作为市场需求量取该组中值的概率(例如![]() ,则取
,则取![]() 的概率等于市场需求量落入
的概率等于市场需求量落入![]() 的频率),求
的频率),求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com