
设C:y=x2(x>0)上的点为P0(x0,y0),过P0作曲线C的切线与x轴交于Q1,过Q1作平行于y轴的直线与曲线C交于P1(x1,y1),然后再过P1作曲线C的切线与x轴交于Q2,过Q2作平行于y轴的直线与曲线C交于P2(x2,y2),依次类推,作出以下各点:Q3,P3,…,Pn,Qn+1,….已知x0=2,设Pn(xn,yn)(n∈N).
(1)设xn=f(n),求f(n)的表达式;
(2)求g(n)=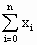 ;
;
(3)设Sn=[g(n)-4]log2f(n).若n>2,求证:-1≤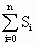 <0.
<0.

|
解 (1)由y=x2得: 设C:直线PnQn+1方程y- 即xn+1= (2)g(n)=2+1+ (3)Sn=[g(n)-4]log2f(n)=-( 令Tn+1= (1)-(2),得 中间n-1项求和,整理得 Tn+1= 所以数列{Tn}是单调递增数列. 因为n>2,所以当n=3时, |


科目:高中数学 来源:高中数学全解题库(国标苏教版·必修4、必修5) 苏教版 题型:044
设P0(x0,y0)为曲线C:y=x2(x>0)上的点,过P0作曲线C的切线与x轴交于点Q1,过Ql作平行于y轴的直线与曲线C交于点P1(xl,y1),然后再过P1作曲线C的切线交x轴于点Q2,过Q2作平行于y轴的直线与曲线C交于点P2(x2,y2),依此类推,作出以下各点:P0,Q1,P1,Q2,P2,Q3,…,Pn,Qn+l,….已知x0=2,设Pn坐标为(xn,yn)(n∈N).
(1)求出过点P0的切线的方程;
(2)设xn=f(n),求f(n)的表达式.
查看答案和解析>>
科目:高中数学 来源:广东仲元中学2007届高三数学质量检测(一) 题型:044
| |||||||||||||||
查看答案和解析>>
科目:高中数学 来源:安徽省池州市2012届高三上学期第一次模试考试数学理科试题 题型:044
设有抛物线C:y=x2,A(1,1)为抛物线C上的一定点,B为抛物线C上异于A的一动点,直线l为抛物线C在A处的切线,点P(2,y0)为直线l上一定点,过点P作直线x轴垂直的直线交直线AB于点Q,交抛物线C于点M,设![]()
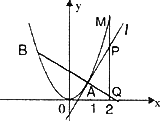
(1)求直线l的方程;
(2)试求λ1-λ2的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江考试院抽学校高三11月抽测测试理科数学试卷(解析版) 题型:解答题
如图,已知曲线C:y=x2(0≤x≤1),O(0,0),Q(1,0),R(1,1).取线段OQ的中点A1,过A1作x轴的垂线交曲线C于P1,过P1作y轴的垂线交RQ于B1,记a1为矩形A1P1B1Q的面积.分别取线段OA1,P1B1的中点A2,A3,过A2,A3分别作x轴的垂线交曲线C于P2,P3,过P2,P3分别作y轴的垂线交A1P1,RB1于B2,B3,记a2为两个矩形A2P2B2 A1与矩形A3P3B3B1的面积之和.以此类推,记an为2n-1个矩形面积之和,从而得数列{an},设这个数列的前n项和为Sn.

(I)求a2与an;
(Ⅱ)求Sn,并证明Sn< .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com