
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源:不详 题型:解答题
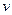 (单位:cm
(单位:cm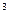 /s)与管道半径
/s)与管道半径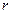 (单位:cm)的四次方成正比.
(单位:cm)的四次方成正比.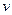 关于管道半径
关于管道半径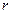 的函数解析式;
的函数解析式;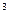 /s,求该气体通过半
/s,求该气体通过半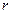 的管道时,其流量速率
的管道时,其流量速率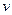 的表达式;
的表达式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 是在
是在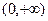 上每一点均可导的函数,若
上每一点均可导的函数,若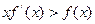 在
在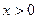 时恒成立.
时恒成立.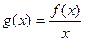 在
在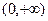 上是增函数;
上是增函数;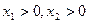 时,有
时,有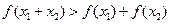 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
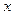 ,
,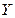 有如下观测数据:
有如下观测数据: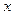 | 7.0 | 4.0 | 8.5 | 9.5 | 3.0 | 1.0 | 8.0 | 5.0 |
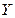 | 11.0 | 8.5 | 13.5 | 15.5 | 4.5 | 3.5 | 13.0 | 7.0 |
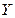 对
对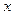 的线性回归方程.
的线性回归方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com