
函数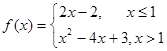 的图象和函数
的图象和函数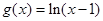 的图象的交点个数是
的图象的交点个数是
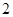
解析试题分析:在同一坐标系内作出y=f(x)和y=g(x)的图象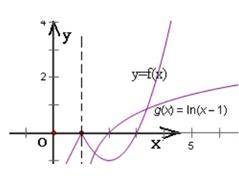
对于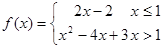 ,
,
当x≤1时,它的图象是直线y=2x-2位于直线x=1左侧的部分;
当x>1时,它的图象是抛物线y=x2-4x+3位于直线x=1右侧部分.
对于g(x)=ln(x-1),
它的图象是对数函数y=lnx的图象右移一个单位而得,
经过定点(2,0)且在直线x=1右侧,以x=1为渐近线呈增函数趋势,
∵当x>1时,点(2,0)位于抛物线张口以内,且g(x)=ln(x-1)经过该点,
∴在直线x=1右侧,两图象有两个交点,
因为函数g(x)=ln(x-1)上所有的点都在x=1右侧,故当x≤1时,两图象没有公式点
综上所述,函数y=f(x)图象和函数g(x)=ln(x-1)的图象有且仅有两个交点
故答案为:2
考点:对数函数的图像与性质;二次函数的图象.
点评:本题给出分段函数和对数函数,求两个函数图象交点的个数,着重考查了基本初等函数的图象与性质等知识,属于基础题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:填空题
关于函数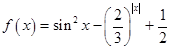 ,
,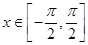 有下面四个结论:
有下面四个结论:
(1) 是奇函数; (2)
是奇函数; (2)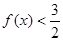 恒成立;
恒成立;
(3) 的最大值是
的最大值是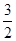 ; (4)
; (4)  的最小值是
的最小值是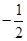 .
.
其中正确结论的是_______________________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com