
【题目】已知F为抛物线E:x2=2py(p>0)的焦点,直线l:y=kx+ ![]() 交抛物线E于A,B两点.
交抛物线E于A,B两点.
(Ⅰ)当k=1,|AB|=8时,求抛物线E的方程;
(Ⅱ)过点A,B作抛物线E的切线l1 , l2 , 且l1 , l2交点为P,若直线PF与直线l斜率之和为﹣ ![]() ,求直线l的斜率.
,求直线l的斜率.
 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,3,则输出v的值为( ) 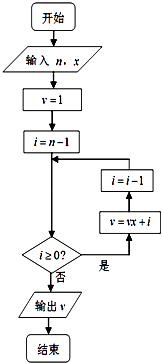
A.20
B.61
C.183
D.548
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 若Sm﹣1=﹣4,Sm=0,Sm+2=14(m≥2,且m∈N*)
(Ⅰ)求m的值;
(Ⅱ)若数列{bn}满足 ![]() =log2bn(n∈N+),求数列{(an+6)bn}的前n项和.
=log2bn(n∈N+),求数列{(an+6)bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的偶函数f(x)在[0,+∞)上递减,若不等式f(x3﹣x2+a)+f(﹣x3+x2﹣a)≥2f(1)对x∈[0,1]恒成立,则实数a的取值范围为( )
A.[ ![]() ,1]
,1]
B.[﹣ ![]() ,1]
,1]
C.[1,3]
D.(﹣∞,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图 
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2017年我国生活垃圾无害化处理量.
参考数据: ![]() =9.32,
=9.32, ![]() =40.17,
=40.17, ![]() =0.55,
=0.55, ![]() ≈2.646.
≈2.646.
参考公式:相关系数r=  回归方程
回归方程 ![]() =
= ![]() +
+ ![]() t 中斜率和截距的最小二乘估计公式分别为:
t 中斜率和截距的最小二乘估计公式分别为: ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(Ⅰ)若曲线y=f(x)与直线y=kx相切于点P,求点P的坐标;
(Ⅱ)当a≤e时,证明:当x∈(0,+∞),f(x)≥a(x﹣lnx).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,4sinA+3cosB=5,4cosA+3sinB=2 ![]() ,则角C等于( )
,则角C等于( )
A.150°或30°
B.120°或60°
C.30°
D.60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com