
【题目】[选修4-4:坐标系与参数方程选讲]在平面直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴,建立极坐标系,曲线C1的参数方程为 ![]() 为参数),曲线C2的极坐标方程为
为参数),曲线C2的极坐标方程为 ![]() .
.
(1)求曲线C1的普通方程和曲线C2的直角坐标方程;
(2)设P为曲线C1上一点,Q曲线C2上一点,求|PQ|的最小值.
科目:高中数学 来源: 题型:
【题目】上海市松江区天马山上的“护珠塔”因其倾斜度超过意大利的比萨斜塔而号称“世界第一斜塔”.兴趣小组同学实施如下方案来测量塔的倾斜度和塔高:如图,记O点为塔基、P点为塔尖、点P在地面上的射影为点H.在塔身OP射影所在直线上选点A,使仰角k∠HAP=45°,过O点与OA成120°的地面上选B点,使仰角∠HPB=45°(点A,B,O都在同一水平面上),此时测得∠OAB=27°,A与B之间距离为33.6米.试求: 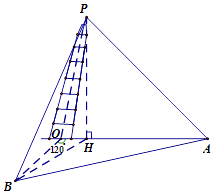
(1)塔高(即线段PH的长,精确到0.1米);
(2)塔身的倾斜度(即PO与PH的夹角,精确到0.1°).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·上海)设z1, z2![]() C, ,则“z1, z2中至少有一个数是虚数”是“z1-z2是虚数”的( )
C, ,则“z1, z2中至少有一个数是虚数”是“z1-z2是虚数”的( )
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.既非充分又非必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,3,则输出v的值为( ) 
A.20
B.61
C.183
D.548
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设曲线y=xn+1(n∈N+)在点(1,1)处的切线与x轴的交点的横坐标为xn , 则log2015x1+log2015x2+…+log2015x2014的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中说法正确的是( )
A.命题“p∨q为真”是命题“p∧q为真”的必要条件
B.向量 ![]() ,
, ![]() 满足
满足 ![]() ,则
,则 ![]() 与
与 ![]() 的夹角为锐角
的夹角为锐角
C.若am2≤bm2 , 则a≤b
D.“?x0∈R,x02﹣x0≤0”的否定是“?x∈R,x2﹣x≥0”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差不为0的等差数列,Sn为数列{an}的前n项和,S5=20,a1 , a3 , a7成等比数列.
(1)求数列{an}的通项公式;
(2)若bn+1=bn+an , 且b1=1,求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为D={x|x≠0},且对于任意x1 , x2∈D,有f(x1x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判断函数f(x)的奇偶性并证明;
(3)如果f(4)=3,f(x﹣2)+f(x+1)≤3,且f(x)在(0,+∞)上是增函数,求实数x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com