
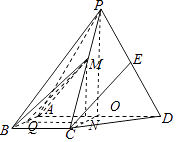
【题目】如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= ![]() AD,∠BAD=∠ABC=90°,E是PD的中点.
AD,∠BAD=∠ABC=90°,E是PD的中点.
(Ⅰ)证明:直线CE∥平面PAB;
(Ⅱ)点M在棱PC 上,且直线BM与底面ABCD所成角为45°,求二面角M﹣AB﹣D的余弦值.
【答案】(Ⅰ)证明:取PA的中点F,连接EF,BF,因为E是PD的中点,
所以EF ![]() AD,AB=BC=
AD,AB=BC= ![]() AD,∠BAD=∠ABC=90°,∴BC∥
AD,∠BAD=∠ABC=90°,∴BC∥ ![]() AD,
AD,
∴BCEF是平行四边形,可得CE∥BF,BF平面PAB,CF平面PAB,
∴直线CE∥平面PAB;
(Ⅱ)解:四棱锥P﹣ABCD中,
侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= ![]() AD,
AD,
∠BAD=∠ABC=90°,E是PD的中点.
取AD的中点O,M在底面ABCD上的射影N在OC上,设AD=2,则AB=BC=1,OP= ![]() ,
,
∴∠PCO=60°,直线BM与底面ABCD所成角为45°,
可得:BN=MN,CN= ![]() MN,BC=1,
MN,BC=1,
可得:1+ ![]() BN2=BN2 , BN=
BN2=BN2 , BN= ![]() ,MN=
,MN= ![]() ,
,
作NQ⊥AB于Q,连接MQ,
所以∠MQN就是二面角M﹣AB﹣D的平面角,MQ= ![]()
= ![]() ,
,
二面角M﹣AB﹣D的余弦值为: ![]() =
= ![]() .
.
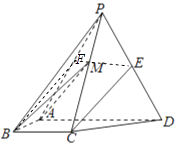
【解析】(Ⅰ)取PA的中点F,连接EF,BF,通过证明CE∥BF,利用直线与平面平行的判定定理证明即可.
(Ⅱ)利用已知条件转化求解M到底面的距离,作出二面角的平面角,然后求解二面角M﹣AB﹣D的余弦值即可.
【考点精析】掌握直线与平面平行的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(12分)
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,∠APD=90°,且四棱锥P﹣ABCD的体积为 ![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直三棱柱ABC﹣A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)是定义在R上的奇函数,对任意的x∈R,满足f(x+1)+f(x)=0,且当0<x<1时,f(x)=2x , 则f(﹣ ![]() )+f(4)= .
)+f(4)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】考察下列命题:其中正确的命题有 ( )
(1)掷两枚硬币,可能出现“两个正面”、“两个反面”、“一正一反”3种结果;
(2)某袋中装有大小均匀的三个红球、二个黑球、一个白球,那么每种颜色的球被摸到的可能性相同;(3)从![]() 中任取一数,取到的数小于0与不小于0的可能性相同;
中任取一数,取到的数小于0与不小于0的可能性相同;
(4)分别从3个男同学、4个女同学中各选一个作代表,那么每个同学当选的可能性相同;
(5)5人抽签,甲先抽,乙后抽,那么乙与甲抽到某号中奖签的可能性肯定不同.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com