练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图是某工厂从工程设计B到试生产H的工序流程图，方框上方的数字为这项工序所用的天数，则从工程设计到结束试生产需要的最短时间为（ ）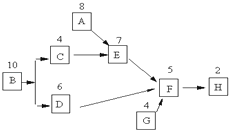

    A.22天
    B.23天
    C.28天
    D.以上都不对

    【答案】C
    【解析】由已知中的工序流程图可得由A到H需要8+7+5+2=22天,由B经C到H需要10+4+7+5+2=28天;由B经D到H需要10+6+5+2=23天;由G到H需要4+5+2=11天;而从工程设计到结束试生产需要的最短时间为这几个时间中的最大值,故从工程设计到结束试生产需要的最短时间为28天,故选C
    本题主要考查了工序流程图（即统筹图），解决问题的关键是由已知中的工序流程图，我们可以计算出每条工程设计从开始到结束的时间，进而根据从工程设计到结束试生产需要的最短时间为这几个时间中的最大值，得到答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （Ⅰ）函数的图象与的图象无公共点，求实数的取值范围；

    （Ⅱ）是否存在实数，使得对任意的，都有函数的图象在的图象的下方？若存在，请求出整数的最大值；若不存在，请说理由.

    （参考数据：，,）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“微信运动”已成为当下热门的健身方式，小王的微信朋友圈内也有大量好友参与了“微信运动”，他随机选取了其中的40人（男、女各20人），记录了他们某一天的走路步数，并将数据整理如下：

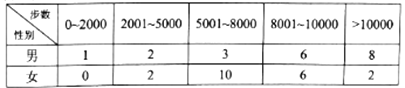
    （1）若采用样本估计总体的方式，试估计小王的所有微信好友中每日走路步数超过5000步的概率；

    （2）已知某人一天的走路步数超过8000步被系统评定“积极型”，否则为“懈怠型”，根据题意完成下面的列联表，并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关？

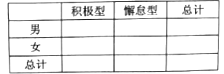    附： ，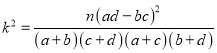

    0．10

    0．05

    0．025

    0．010

    2．706

    3．841

    5．024

    6．635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中，底面为菱形， 底面， ， 是上的一点，PE=2EC， 为的中点.

    （1）证明： 平面；

    （2）证明： 平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数y=f（x）在R上可导且满足不等式xf′（x）+f（x）＞0恒成立，且常数a，b满足a＞b，则下列不等式一定成立的是（ ）
    A.af（a）＞bf（b）
    B.af（b）＞bf（a）
    C.af（a）＜bf（b）
    D.af（b）＜bf（a）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设计一个尺规作图的算法来确定线段AB的一个五等分点，并画出流程图。
    （点拨：确定线段AB的五等分点，是指在线段AB上确定一点M，使得 ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

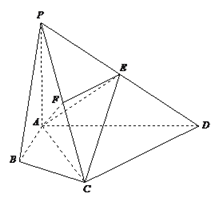
    【题目】四棱锥P－ABCD中，∠ABC＝∠ACD＝90°，∠BAC＝∠CAD＝60°，PA⊥平面ABCD，

    E为PD的中点，PA＝2AB＝2．

    （1）若F为PC的中点，求证PC⊥平面AEF；

    （2）求二面角的平面角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）

    已知函数， ,且函数在处的切线平行于直线．

    （Ⅰ）实数的值；（Ⅱ）若在（）上存在一点，使得成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，M，N，K分别是正方体ABCD﹣A1B1C1D1的棱AB，CD，C1D1的中点．

    （1）求证：AN∥平面A1MK；
    （2）求证：平面A1B1C⊥平面A1MK．

    查看答案和解析>>

    同步练习册答案