
【题目】【2016高考天津文数】某化肥厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示:
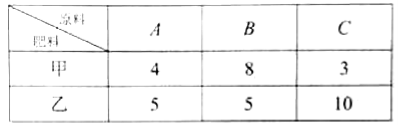
现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x,y计划表示生产甲、乙两种肥料的车皮数.
(Ⅰ)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?并求出此最大利润.
【答案】(Ⅰ)详见解析;(Ⅱ)生产甲种肥料![]() 车皮,乙种肥料
车皮,乙种肥料![]() 车皮时利润最大,且最大利润为
车皮时利润最大,且最大利润为![]() 万元
万元
【解析】
试题分析:(Ⅰ)根据生产原料不能超过A种原料200吨,B种原料360吨,C种原料300吨,列不等关系式,即可行域,再根据直线及区域画出可行域;(Ⅱ)目标函数为利润![]() ,根据直线平移及截距变化规律确定最大利润.
,根据直线平移及截距变化规律确定最大利润.
试题解析:(Ⅰ)解:由已知,![]() 满足的数学关系式为
满足的数学关系式为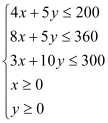 ,该二元一次不等式组所表示的平面区域为下图中的阴影部分:
,该二元一次不等式组所表示的平面区域为下图中的阴影部分:

(图 1)
(Ⅱ)解:设利润为![]() 万元,则目标函数为
万元,则目标函数为![]() .考虑z=2x+3y,将它变形为
.考虑z=2x+3y,将它变形为![]() ,这是斜率为
,这是斜率为![]() ,随
,随![]() 变化的一族平行直线.
变化的一族平行直线.![]() 为直线在
为直线在![]() 轴上的截距,当
轴上的截距,当![]() 取最大值时,
取最大值时,![]() 的值最大.又因为
的值最大.又因为![]() 满足约束条件,所以由图2可知,当直线
满足约束条件,所以由图2可知,当直线![]() 经过可行域上的点
经过可行域上的点![]() 时,截距
时,截距![]() 最大,即
最大,即![]() 最大.解方程组
最大.解方程组![]() ,得点
,得点![]() 的坐标为
的坐标为![]() ,所以
,所以![]() .
.
答:生产甲种肥料![]() 车皮、乙种肥料
车皮、乙种肥料![]() 车皮时利润最大,且最大利润为
车皮时利润最大,且最大利润为![]() 万元.
万元.
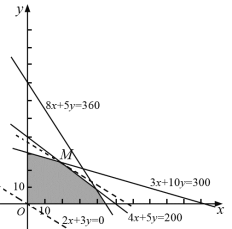
(图 2)


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,过点A(﹣6,0)的直线l1与直线l2:y=2x相交于点B(m,4).
(1)求直线l1的表达式;
(2)过动点P(n,0)且垂于x轴的直线与l1 , l2的交点分别为C,D,当点C位于点D上方时,写出n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b﹣2c)cosA=a﹣2acos2 ![]() .
.
(1)求角A的值;
(2)若a= ![]() ,则求b+c的取值范围.
,则求b+c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1+sin2x,sinx﹣cosx),
=(1+sin2x,sinx﹣cosx), ![]() =(1,sinx+cosx),函数f(x)=
=(1,sinx+cosx),函数f(x)= ![]()
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的最大值及取得最大值相应的x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心
的圆心![]() 在
在![]() 轴上,半径为1,直线
轴上,半径为1,直线![]() 被圆
被圆![]() 所截的弦长为
所截的弦长为![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 的下方.
的下方.
(1)求圆![]() 的方程;
的方程;
(2)设![]() ,若圆
,若圆![]() 是
是![]() 的内切圆,求
的内切圆,求![]() 的面积
的面积![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究学生在考试时做解答题的情况,老师从甲、乙两个班级里各随机抽取了五份答卷并对解答题第16题(满分13分)的得分进行统计,得到对应的甲、乙两组数据,其茎叶图如图所示,其中x,y∈{0,1,2,3},已知甲组数据的中位数比乙组数据的平均数多 ![]() ,则x+y的值为( )
,则x+y的值为( ) 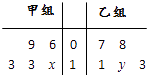
A.5
B.4
C.3
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“北祠堂”是我校著名的一支学生乐队,对于2015年我校“校园周末文艺广场”活动中“北祠堂”乐队的表现,在高一年级学生中投票情况的统计结果见表:
喜爱程度 | 非常喜欢 | 一般 | 不喜欢 |
人数 | 500 | 200 | 100 |
现采用分层抽样的方法从所有参与对“北祠堂”投票的800名学生中抽取一个容量为n的样本,若从不喜欢“北祠堂”的100名学生中抽取的人数是5人.
(1)求n的值;
(2)若从不喜欢“北祠堂”的学生中抽取的5人中恰有3名男生(记为a1 , a2 , a3)2名女生(记为b1 , b2),现将此5人看成一个总体,从中随机选出2人,列出所有可能的结果;
(3)在(2)的条件下,求选出的2人中至少有1名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com