
【题目】关于函数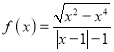 的性质描述,正确的是__________.①
的性质描述,正确的是__________.①![]() 的定义域为
的定义域为![]() ;②
;②![]() 的值域为
的值域为![]() ;③
;③![]() 的图象关于原点对称;④
的图象关于原点对称;④![]() 在定义域上是增函数.
在定义域上是增函数.
【答案】①②③
【解析】
由被开方式非负和分母不为0,解不等式可得f(x)的定义域,可判断①;化简f(x),讨论0<x≤1,﹣1≤x<0,分别求得f(x)的范围,求并集可得f(x)的值域,可判断②;由f(﹣1)=f(1)=0,f(x)不是增函数,可判断④;由奇偶性的定义得f(x)为奇函数,可判断③.
①,由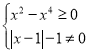 ,解得﹣1≤x≤1且x≠0,
,解得﹣1≤x≤1且x≠0,
可得函数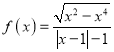 的定义域为[﹣1,0)∪(0,1],故①正确;
的定义域为[﹣1,0)∪(0,1],故①正确;
②,由①可得f(x)=![]() ,即f(x)=﹣
,即f(x)=﹣![]() ,
,
当0<x≤1可得f(x)=﹣![]() ∈(﹣1,0];当﹣1≤x<0可得f(x)=
∈(﹣1,0];当﹣1≤x<0可得f(x)=![]() ∈[0,1).
∈[0,1).
可得f(x)的值域为(﹣1,1),故②正确;
③,由f(x)=﹣![]() 的定义域为[﹣1,0)∪(0,1],关于原点对称,
的定义域为[﹣1,0)∪(0,1],关于原点对称,
f(﹣x)=![]() =﹣f(x),则f(x)为奇函数,即有f(x)的图象关于原点对称,故③正确.
=﹣f(x),则f(x)为奇函数,即有f(x)的图象关于原点对称,故③正确.
④,由f(﹣1)=f(1)=0,则f(x)在定义域上不是增函数,故④错误;
故答案为:①②③


科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随即抽取![]() 人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的
人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的![]() 人中的性别以及意见进行了分类,得到的数据如下表所示:
人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)根据表中的数据,能否在犯错误的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(2)现按照分层抽样从认为共享产品增多对生活无益的人员中随机抽取![]() 人,再从
人,再从![]() 人中随机抽取
人中随机抽取![]() 人赠送超市购物券作为答谢,求恰有
人赠送超市购物券作为答谢,求恰有![]() 人是女性的概率.
人是女性的概率.
参与公式: 
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (实数
(实数![]() 为常数)
为常数)
(1)当![]() 时,证明
时,证明![]() 在
在![]() 上单调递减;
上单调递减;
(2)若![]() ,且
,且![]() 为偶函数,求实数
为偶函数,求实数![]() 的值;
的值;
(3)小金同学在求解函数![]() 的对称中心时,发现函数
的对称中心时,发现函数![]() 是一个复合函数,设
是一个复合函数,设![]() ,
,![]() ,则
,则![]() ,显然
,显然![]() 有对称中心,设为
有对称中心,设为![]() ,
,![]() 有反函数
有反函数![]() ,则
,则![]() 的对称中心为
的对称中心为![]() ,请问小金的做法是否正确?如果正确,请给出证明,并直接写出当
,请问小金的做法是否正确?如果正确,请给出证明,并直接写出当![]() 时
时![]() 的对称中心;如果错误,请举出反例,并用正确的方法直接写出当
的对称中心;如果错误,请举出反例,并用正确的方法直接写出当![]() 时
时![]() 的对称中心.
的对称中心.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() 、
、![]() 为已知实常数,
为已知实常数,![]() .
.
下列所有正确命题的序号是____________.
①若![]() ,则
,则![]() 对任意实数
对任意实数![]() 恒成立;
恒成立;
②若![]() ,则函数
,则函数![]() 为奇函数;
为奇函数;
③若![]() ,则函数
,则函数![]() 为偶函数;
为偶函数;
④当![]() 时,若
时,若![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题P:不等式![]() 的解集中的整数有且仅有-1,0,1.求a的取值范围.
的解集中的整数有且仅有-1,0,1.求a的取值范围.
命题Q:集合![]() 且
且![]() .
.
(1)分别求命题P、Q为真命题时的实数a的取值范围;
(2)当实数a取何值时,命题P、Q中有且仅有一个为真命题;
(3)设P、Q皆为真时a的取值范围为集合S,![]() ,若全集
,若全集![]() ,
,![]() ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于两个变量x和y进行回归分析,得到一组样本数据:![]() 则下列说法不正确的是( )
则下列说法不正确的是( )
A.由样本数据得到的回归直线![]() 必经过样本点中心
必经过样本点中心![]()
B.残差平方和越小的模型,拟合的效果越好
C.用![]() 来刻画回归效果,
来刻画回归效果,![]() 的值越小,说明模型的拟合效果越好
的值越小,说明模型的拟合效果越好
D.若变量y和x之间的相关系数![]() ,则变量y和x之间具有线性相关关系
,则变量y和x之间具有线性相关关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x),当x≥0时,f(x)=x2﹣x.
(1)求函数f(x)的解析式;
(2)若函数g(x)![]() (x≠0),求证:函数g(x)在(0,+∞)单调递增.
(x≠0),求证:函数g(x)在(0,+∞)单调递增.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com