
【题目】如图,在四棱锥P-ABCD中,AD∥BC,![]() ADC=
ADC=![]() PAB=90°,BC=CD=
PAB=90°,BC=CD=![]() AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.

(I)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(II)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:本题考查线面平行、线线平行、向量法等基础知识,考查空间想象能力、分析问题的能力、计算能力.第一问,利用线面平行的定理,先证明线线平行,再证明线面平行;第二问,可以先找到线面角,再在三角形中解出正弦值,还可以用向量法建立直角坐标系解出正弦值.
试题解析:(Ⅰ)在梯形ABCD中,AB与CD不平行.
延长AB,DC,相交于点M(M∈平面PAB),点M即为所求的一个点.理由如下:
由已知,BC∥ED,且BC=ED.
所以四边形BCDE是平行四边形.
从而CM∥EB.
又EB![]() 平面PBE,CM
平面PBE,CM![]() 平面PBE,
平面PBE,
所以CM∥平面PBE.
(说明:延长AP至点N,使得AP=PN,则所找的点可以是直线MN上任意一点)
(Ⅱ)方法一:
由已知,CD⊥PA,CD⊥AD,PA![]() AD=A,
AD=A,
所以CD⊥平面PAD.
从而CD⊥PD.
所以![]() PDA是二面角P-CD-A的平面角.
PDA是二面角P-CD-A的平面角.
所以![]() PDA=45°.
PDA=45°.
设BC=1,则在Rt△PAD中,PA=AD=2.
过点A作AH⊥CE,交CE的延长线于点H,连接PH.
易知PA⊥平面ABCD,
从而PA⊥CE.
于是CE⊥平面PAH.
所以平面PCE⊥平面PAH.
过A作AQ⊥PH于Q,则AQ⊥平面PCE.
所以![]() APH是PA与平面PCE所成的角.
APH是PA与平面PCE所成的角.
在Rt△AEH中,![]() AEH=45°,AE=1,
AEH=45°,AE=1,
所以AH=![]() .
.
在Rt△PAH中,PH=![]() =
=![]() ,
,
所以sin![]() APH=
APH=![]() =
=![]() .
.

方法二:
由已知,CD⊥PA,CD⊥AD,PA![]() AD=A,
AD=A,
所以CD⊥平面PAD.
于是CD⊥PD.
从而![]() PDA是二面角P-CD-A的平面角.
PDA是二面角P-CD-A的平面角.
所以![]() PDA=45°.
PDA=45°.
由PA⊥AB,可得PA⊥平面ABCD.
设BC=1,则在Rt△PAD中,PA=AD=2.
作Ay⊥AD,以A为原点,以![]() ,
,![]() 的方向分别为x轴,z轴的正方向,建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),P(0,0,2),C(2,1,0),E(1,0,0),
的方向分别为x轴,z轴的正方向,建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),P(0,0,2),C(2,1,0),E(1,0,0),
所以![]() =(1,0,-2),
=(1,0,-2),![]() =(1,1,0),
=(1,1,0),![]() =(0,0,2)
=(0,0,2)
设平面PCE的法向量为n=(x,y,z),
由 得
得![]() 设x=2,解得n=(2,-2,1).
设x=2,解得n=(2,-2,1).
设直线PA与平面PCE所成角为α,则sinα=![]() =
=![]() .
.
所以直线PA与平面PCE所成角的正弦值为![]() .
.



 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】设p:A={x|2x2﹣3ax+a2<0},q:B={x|x2+3x﹣10≤0}.
(1)求A;
(2)当a<0时,若¬p是¬q的必要不充分条件,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
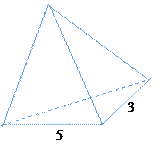
【题目】如图所示,某几何体的三视图都是直角三角形,则该几何体的体积等于__________.
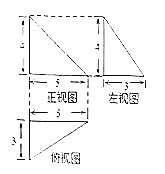
【答案】10
【解析】几何体为三棱锥,(高为4,底面为直角三角形),体积为![]()
点睛:空间几何体体积问题的常见类型及解题策略
(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解.
(2)若所给定的几何体的体积不能直接利用公式得出,则常用转换法、分割法、补形法等方法进行求解.
(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,然后根据条件求解.
【题型】填空题
【结束】
15
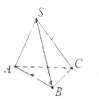
【题目】如图:在三棱锥![]() 中,已知底面
中,已知底面![]() 是以
是以![]() 为斜边的等腰直角三角形,且侧棱长
为斜边的等腰直角三角形,且侧棱长![]() ,则三棱锥
,则三棱锥![]() 的外接球的表面积等于__________.
的外接球的表面积等于__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4﹣1:几何证明选讲
如图,⊙O和⊙O′相交于A,B两点,过A作两圆的切线分别交两圆于C、D两点,连接DB并延长交⊙O于点E.证明:
(1)ACBD=ADAB;
(2)AC=AE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义非零向量![]() 的“相伴函数”为
的“相伴函数”为![]() (
(![]() ),向量
),向量![]() 称为函数
称为函数![]() 的“相伴向量”(其中
的“相伴向量”(其中![]() 为坐标原点),记平面内所有向量的“相伴函数”构成的集合为
为坐标原点),记平面内所有向量的“相伴函数”构成的集合为![]() .
.
(1)已知![]() (
(![]() ),求证:
),求证:![]() ,并求函数
,并求函数![]() 的“相伴向量”模的取值范围;
的“相伴向量”模的取值范围;
(2)已知点![]() (
(![]() )满足
)满足![]() ,向量
,向量![]() 的 “相伴函数”
的 “相伴函数”![]() 在
在![]() 处取得最大值,当点
处取得最大值,当点![]() 运动时,求
运动时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在空间四边形ABCD中,点E,H分别是边AB,AD的中点,点F,G分别是边BC,CD上的点,且![]() ,则下列说法正确的是________.(填写所有正确说法的序号)
,则下列说法正确的是________.(填写所有正确说法的序号)

①EF与GH平行; ②EF与GH异面;
③EF与GH的交点M可能在直线AC上,也可能不在直线AC上;
④EF与GH的交点M一定在直线AC上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数f(x)=(x+l)lnx﹣ax+a (a为正实数,且为常数)
(1)若f(x)在(0,+∞)上单调递增,求a的取值范围;
(2)若不等式(x﹣1)f(x)≥0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x∈(0, ![]() ),则函数f(x)=sinxtanx+cosxcotx的值域为( )
),则函数f(x)=sinxtanx+cosxcotx的值域为( )
A.[1,2)
B.[ ![]() ,+∞)
,+∞)
C.(1, ![]() ]
]
D.[1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com