
【题目】函数f (x)=![]() (-6≤x≤10)的所有零点之和为____________.
(-6≤x≤10)的所有零点之和为____________.
【答案】16
【解析】
构造函数g(x)=(![]() )|x﹣2|,h(x)=﹣2cos
)|x﹣2|,h(x)=﹣2cos![]() ,由于﹣6≤x≤10时,函数g(x),h(x)的图象都关于直线x=2对称,可得函数f(x)在﹣6≤x≤10的图象关于直线x=2对称.运用﹣6≤x≤10时,函数g(x),h(x)的图象的交点共有8个,即可得到f(x)的所有零点之和.
,由于﹣6≤x≤10时,函数g(x),h(x)的图象都关于直线x=2对称,可得函数f(x)在﹣6≤x≤10的图象关于直线x=2对称.运用﹣6≤x≤10时,函数g(x),h(x)的图象的交点共有8个,即可得到f(x)的所有零点之和.
构造函数g(x)=(![]() )|x﹣2|,
)|x﹣2|,
h(x)=﹣2cos![]() ,
,
∵﹣6≤x≤10时,
函数g(x),h(x)的图象
都关于直线x=2对称,
∴函数f(x)=(![]() )|x﹣2|+2cos
)|x﹣2|+2cos![]()
(﹣6≤x≤10)
的图象关于直线x=2对称.
∵﹣6≤x≤10时,函数g(x),h(x)的图象的交点共有8个,
∴函数f(x)的所有零点之和等于4×4=16.
故答案为:16.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以平面直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程是
的参数方程是![]() ,(
,(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,且对任意的
,且对任意的![]() 有
有![]() . 当
. 当![]() 时,
时,![]() ,
,![]() .
.
(1)求![]() 并证明
并证明![]() 的奇偶性;
的奇偶性;
(2)判断![]() 的单调性并证明;
的单调性并证明;
(3)求![]() ;若
;若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),圆
为参数),圆![]() 与圆
与圆![]() 外切于原点
外切于原点![]() ,且两圆圆心的距离
,且两圆圆心的距离![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求圆![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)过点![]() 的直线
的直线![]() 与圆
与圆![]() 异于点
异于点![]() 的交点分别为点
的交点分别为点![]() ,与圆
,与圆![]() 异于点
异于点![]() 的交点分别为点
的交点分别为点![]() ,且
,且![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B是半径为2的圆周上的定点,P为圆周上的动点,![]() 是锐角,大小为β.图中阴影区域的面积的最大值为
是锐角,大小为β.图中阴影区域的面积的最大值为
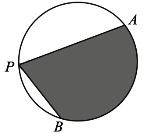
A. 4β+4cosβB. 4β+4sinβC. 2β+2cosβD. 2β+2sinβ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=![]() PD.
PD.

(I)证明:平面PQC⊥平面DCQ
(II)求二面角Q-BP-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天津大学某学院欲安排4名毕业生到某外资企业的三个部门![]() 实习,要求每个部门至少安排1人,其中甲大学生不能安排到
实习,要求每个部门至少安排1人,其中甲大学生不能安排到![]() 部门工作的方法有_______种(用数字作答).
部门工作的方法有_______种(用数字作答).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com