【题目】已知函数f（x）=（2x﹣
）x，则下列结论中正确的是（ ）
A.若﹣3≤m＜n，则f（m）＜f（n）
B.若m＜n≤0，则f（m）＜f（n）
C.若f（m）＜f（n），则m2＜n2
D.若f（m）＜f（n），则m3＜n3
【答案】C
【解析】函数f（x）=（2x﹣
）x的定义域为R，
f（﹣x）=（2﹣x﹣2x）（﹣x）=x（2x﹣2﹣x）=f（x），
则f（x）为偶函数，
f（x）的导数f′（x）=x（2xln2+2﹣xln2）+2x﹣2﹣x ，
当x＞0时，2x＞1，0＜2﹣x＜1，则f′（x）＞0，f（x）在（0，+∞）递增，
则由偶函数的性质，可得f（x）在（﹣∞，0]上递减．
对于A，若﹣3≤m＜n，有f（m）＞f（n），A不正确；
对于B，若m＜n≤0，则f（m）＞f（n），B不正确；
对于C，若f（m）＜f（n），即为f（|m|）＜f（|n|），则有|m|＜|n|，
即有m2＜n2 ， C正确；
对于D，若f（m）＜f（n），则m，n不好比较大小，则D不正确．
故选C．
金状元绩优好卷系列答案科目：高中数学 来源： 题型：
【题目】在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，其中AD∥BC，AB⊥AD，AB=AD= 
BC， 
= 
． 
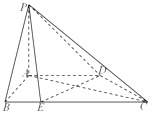
（1）求证：DE⊥平面PAC；
（2）若直线PE与平面PAC所成角的正弦值为 
，求二面角A﹣PC﹣D的平面角的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】数列{an}共有5项，其中a1=0，a5=2，且|ai+1﹣ai|=1，i=1，2，3，4，则满足条件的不同数列的个数为（ ）
A.3
B.4
C.5
D.6
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
（其中a∈R）．
（1）讨论函数f（x）的奇偶性，并说明理由．
（2）若
，试判断函数f（x）在区间[1，+∞）上的单调性，并用函数单调性定义给出证明．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义域为R的函数f（x）满足：对于任意的实数x，y都有f（x+y）=f（x）+f（y）成立，且当x＜0时，f（x）＞0恒成立，且nf（x）=f（nx）．（n是一个给定的正整数）．
（1）判断函数f（x）的奇偶性，并证明你的结论；
（2）证明f（x）为减函数；若函数f（x）在[-2，5]上总有f（x）≤10成立，试确定f（1）应满足的条件；
（3）当a＜0时，解关于x的不等式
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在四棱柱ABCD－A1B1C1D1中，
,平面BB1C1C
底面ABCD，点
、F分别是线段
、BC的中点．
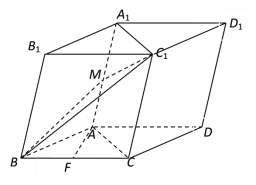
（1）求证：AF//平面
；
（2）求证：平面BB1C1C⊥平面．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出下列五个命题：
①函数f（x）=2a2x-1-1的图象过定点（
，-1）；
②已知函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=x（x+1），若f（a）=-2则实数a=-1或2．
③若loga＞1，则a的取值范围是（，1）；
④若对于任意x∈R都f（x）=f（4-x）成立，则f（x）图象关于直线x=2对称；
⑤对于函数f（x）=lnx，其定义域内任意x1≠x2都满足f（
）≥
其中所有正确命题的序号是______．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
