
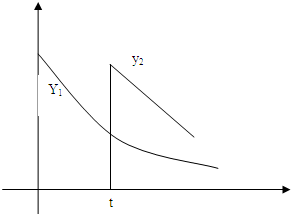 ����ѧ���о�ijλѧ����ѧϰ������֣�����λѧ����ѧ���֪ʶ������Ϊ1����x���Ĵ�����y1=
����ѧ���о�ijλѧ����ѧϰ������֣�����λѧ����ѧ���֪ʶ������Ϊ1����x���Ĵ�����y1=| 4 |
| x+4 |
| a |
| (t+4)2 |
| a |
| (t+4)2 |
| 8 |
| t+4 |
| 4 |
| x+4 |
| a |
| (t+4)2 |
| 8 |
| t+4 |
| 4 |
| x+4 |
| a |
| (t+4)2 |
| 8 |
| t+4 |
| 4 |
| x+4 |
| -1 |
| (5+4)2 |
| 8 |
| 5+4 |
| 4 |
| x+4 |
| -(x+4) |
| 81 |
| 4 |
| x+4 |
|
| 5 |
| 9 |
| a |
| (t+4)2 |
| 8 |
| t+4 |
| 4 |
| x+4 |
| -a(x+4) |
| (t+4)2 |
| 4 |
| x+4 |
| 8 |
| t+4 |
| a(t+4) |
| (t+4)2 |
|
| 8-a |
| t+4 |
| -a(x+4) |
| (t+4)2 |
| 4 |
| x+4 |
| 2 | ||
|
| 2 | ||
|
| ab |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2011-2012ѧ�꽭��ʡ������ѧ�����������ѧ�Ծ� ���ͣ������
����ѧ���о�ijλѧ����ѧϰ������֣�����λѧ����ѧ���֪ʶ��������Ϊ1����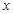 ���Ĵ�����
���Ĵ�����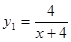 ������
������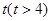 ��ʱ���е�һ�θ�ϰ�����ʱ֪ʶ��������δ��ϰ���������һ������ϰʱ����Բ��ƣ������洢��
��ʱ���е�һ�θ�ϰ�����ʱ֪ʶ��������δ��ϰ���������һ������ϰʱ����Բ��ƣ������洢��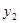 ��ʱ��仯������ǡΪֱ�ߵ�һ���֣���б��Ϊ
��ʱ��仯������ǡΪֱ�ߵ�һ���֣���б��Ϊ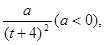 ��������ʱ��仯��������ͼ��ʾ.�����е�һ�θ�ϰ��Ĵ������벻��ϰ�Ĵ�����������ʱ����ƴ�ʱ�˿�Ϊ�����θ�ϰ���ʱ���㡱.
��������ʱ��仯��������ͼ��ʾ.�����е�һ�θ�ϰ��Ĵ������벻��ϰ�Ĵ�����������ʱ����ƴ�ʱ�˿�Ϊ�����θ�ϰ���ʱ���㡱.
��1����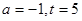 ���������ʱ���㡱��
���������ʱ���㡱��
��2���������ˡ����θ�ϰ���ʱ���㡱����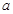 ��ȡֵ��Χ.
��ȡֵ��Χ.
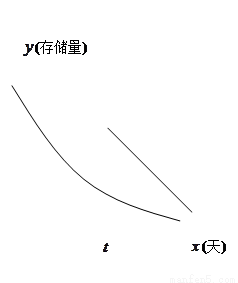
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�꽭��ʡ�ձ����и߿���ѧ��ģ�Ծ��������棩 ���ͣ������
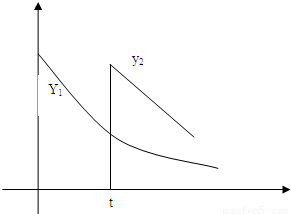 ����ѧ���о�ijλѧ����ѧϰ������֣�����λѧ����ѧ���֪ʶ������Ϊ1����x ���Ĵ�����
����ѧ���о�ijλѧ����ѧϰ������֣�����λѧ����ѧ���֪ʶ������Ϊ1����x ���Ĵ�����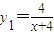 ������t��t��0����ʱ���е�һ�θ�ϰ�����ʱ���ƺ���������δ��ϰ���������һ������ϰ��ʱ����Բ��ƣ�����������y2��ʱ��仯������ǡ��Ϊֱ�ߵ�һ���֣���б��Ϊ
������t��t��0����ʱ���е�һ�θ�ϰ�����ʱ���ƺ���������δ��ϰ���������һ������ϰ��ʱ����Բ��ƣ�����������y2��ʱ��仯������ǡ��Ϊֱ�ߵ�һ���֣���б��Ϊ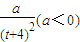 ����������ʱ��仯��������ͼ��ʾ�������е�һ�θ�ϰ��Ĵ������벻��ϰ�Ĵ�����������ʱ����ƴ�ʱ��Ϊ�����θ�ϰ���ʱ���㡱
����������ʱ��仯��������ͼ��ʾ�������е�һ�θ�ϰ��Ĵ������벻��ϰ�Ĵ�����������ʱ����ƴ�ʱ��Ϊ�����θ�ϰ���ʱ���㡱�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com