



 ,
, 的坐标,最后由夹角公式计算异面直线AB和CD所成角的余弦值即可
的坐标,最后由夹角公式计算异面直线AB和CD所成角的余弦值即可 设等边三角形的边长为2.
设等边三角形的边长为2. ),B(0,-1,0),C(0,1,0),D(
),B(0,-1,0),C(0,1,0),D( ,0,0)
,0,0) =(0,-1,-
=(0,-1,- ),
),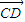 =(
=( ,-1,0)
,-1,0)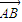 ,
, >=
>= =
= =
=



 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源:浙江省金华一中2012届高三上学期期中考试数学文科试题(人教版) 题型:013
有共同底边的等边三角形ABC和BCD所在平面互相垂直,则异面直线AB和CD所成角的余弦值为
A.0
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源:2010-2011年四川省成都市高二3月月考数学试卷 题型:选择题
(理科)有共同底边的等边三角形 和
和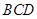 所在平面互相垂直,则异面直线
所在平面互相垂直,则异面直线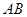 和
和 所成角的余弦值为
( )
所成角的余弦值为
( )
A. B.
B.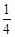 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省金华一中高三(上)期中数学试卷(文科)(解析版) 题型:选择题



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com