
分析 将原式的分子分母同时除以n2003得$\frac{\frac{1}{{n}^{2003}}+\frac{2}{{n}^{2002}}+\frac{3}{{n}^{2001}}+…+\frac{1}{{n}^{0}}•2004}{1+\frac{2}{n}+\frac{3}{{n}^{2}}+…+\frac{2004}{{n}^{2003}}}$,再直接取其极限即可.
解答 解:将原式的分子分母同时除以n2003,
原式=$\underset{lim}{n→∞}$$\frac{1+2n+3{n}^{2}+…+2004{n}^{2003}}{{n}^{2003}+2{n}^{2002}+…+2003n+2004}$
=$\underset{lim}{n→∞}$$\frac{\frac{1}{{n}^{2003}}+\frac{2}{{n}^{2002}}+\frac{3}{{n}^{2001}}+…+\frac{1}{{n}^{0}}•2004}{1+\frac{2}{n}+\frac{3}{{n}^{2}}+…+\frac{2004}{{n}^{2003}}}$,
其中,$\underset{lim}{n→∞}$$\frac{1}{{n}^{k}}$=0,k=1,2,3,…,2003,
所以,原式=$\frac{0+0+0+…+0+2004}{1+0+0+…+0+0}$=2004.
故答案为:2004.
点评 本题主要考查了数列极限及其运算,将分式的分子分母同时除以n的最高次数项是解决本题的关键,属于中档题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
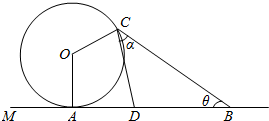 如图,在一条景观道的一端有一个半径为50米的圆形摩天轮O,逆时针15分钟转一圈,从A处进入摩天轮的座舱,OA垂直于地面AM,在距离A处150米处设置了一个望远镜B.
如图,在一条景观道的一端有一个半径为50米的圆形摩天轮O,逆时针15分钟转一圈,从A处进入摩天轮的座舱,OA垂直于地面AM,在距离A处150米处设置了一个望远镜B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
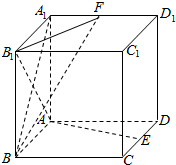 如图,在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com