
【题目】已知函数![]() ,
,![]() .
.
(1)讨论函数![]() 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)设![]() ,若不等式
,若不等式![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先对函数求导,然后对![]() 讨论.当
讨论.当![]() 时,
时,![]() 在
在![]() 上恒成立,函数
上恒成立,函数![]() 在
在![]() 单调递增,∴
单调递增,∴![]() 在
在![]() 上没有极值点.当
上没有极值点.当![]() 时,
时,![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,即
上递增,即![]() 在
在![]() 处有极小值,无极大值.
处有极小值,无极大值.
(2)设![]() ,不等式
,不等式![]() 对任意
对任意![]() 恒成立,即函数
恒成立,即函数![]() 在
在![]() 上的最小值大于零.所以求出
上的最小值大于零.所以求出![]() 的最小值,由最小值大于零求出
的最小值,由最小值大于零求出![]() 的取值范围.
的取值范围.
试题解析:(1)![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,
函数![]() 在
在![]() 单调递增,∴
单调递增,∴![]() 在
在![]() 上没有极值点.
上没有极值点.
当![]() 时,
时,![]() 得
得![]() ,
,![]() 得
得![]() ,
,
∴![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,即
上递增,即![]() 在
在![]() 处有极小值,无极大值.
处有极小值,无极大值.
∴当![]() 时,
时,![]() 在
在![]() 上没有极值点,
上没有极值点,
当![]() 时,
时,![]() 在
在![]() 上有一个极值点.
上有一个极值点.
(2)设![]()
![]() ,
,
![]()
![]() ,
,
不等式![]() 对任意
对任意![]() 恒成立,即函数
恒成立,即函数![]() 在
在![]() 上的最小值大于零.
上的最小值大于零.
①当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() 的最小值为
的最小值为![]() ,
,
由![]() 可得
可得![]() ,
,
因为![]() ,所以
,所以![]() .
.
②当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 最小值为
最小值为![]() ,由
,由![]() 可得
可得![]() ,即
,即![]() .
.
③当![]() ,即
,即![]() 时,可得
时,可得![]() 最小值为
最小值为![]() ,
,
因为![]() ,所以
,所以![]() ,
,
故![]() .
.
即![]() ,
,
综上可得,![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】设人的某一特征(如眼睛的大小)是由他的一对基因所决定,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人为纯隐性,具有rd基因的人为混合性,纯显性与混合性的人都显露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性,问:
(1)1个孩子显露显性特征的概率是多少?
(2)“该父母生的2个孩子中至少有1个显露显性特征”,这种说法正确吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)向量a=(x,1),b=(1,y),c=(2,-4),且a⊥c,b∥c,求|a+b|和a+b与c的夹角;
(2)设O为△ABC的外心,已知AB=3,AC=4,非零实数x,y满足![]() =x
=x![]() +y
+y![]() ,且x+2y=1,求cos ∠BAC的值.
,且x+2y=1,求cos ∠BAC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国个人所得税法》规定,公民全月工资所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额,此项税款按下表分段累计计算:

(1)某人10月份应交此项税款为350元,则他10月份的工资收入是多少?
(2)假设某人的月收入为![]() 元,
元, ![]() ,记他应纳税为
,记他应纳税为![]() 元,求
元,求![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知曲线C1的参数方程为![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为![]() .
.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与
轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为![]() ,且各局胜负相互独立,求:
,且各局胜负相互独立,求:
(1)打满3局比赛还未停止的概率;
(2)比赛停止时已打局数ξ的分布列与期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班为了提高学生学习英语的兴趣,在班内举行英语写、说、唱综合能力比赛,比赛分为预赛和决赛2个阶段,预赛为笔试,决赛为说英语、唱英语歌曲,将所有参加笔试的同学(成绩得分为整数,满分100分)进行统计,得到频率分布直方图,其中后三个矩形高度之比依次为4:2:1,落在![]() 的人数为12人.
的人数为12人.
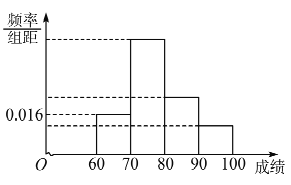
(Ⅰ)求此班级人数;
(Ⅱ)按规定预赛成绩不低于90分的选手参加决赛,已知甲乙两位选手已经取得决赛资格,参加决赛的选手按抽签方式决定出场顺序.
(i)甲不排在第一位乙不排在最后一位的概率;
(ii)记甲乙二人排在前三位的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com