
 =
=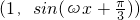 ,
, =
=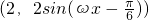 (其中ω为正常数)
(其中ω为正常数)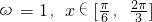 ,求
,求 ∥
∥ 时tanx的值;
时tanx的值; •
• -2,若函数f(x)的图象的相邻两个对称中心的距离为
-2,若函数f(x)的图象的相邻两个对称中心的距离为 ,求f(x)在区间
,求f(x)在区间 上的最小值.
上的最小值. ∥
∥ 时,
时, ,(2分)
,(2分)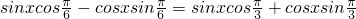
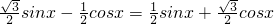 (4分)
(4分)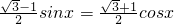 ,
,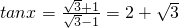 (6分)
(6分) =
=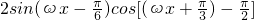 =
=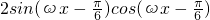 =
=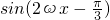 .(9分)
.(9分) =
= =
=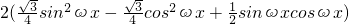 =
= (9分)
(9分)
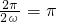 ,解之,得ω=1.(11分)
,解之,得ω=1.(11分) .
. ,所以
,所以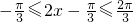 .
.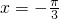 时,f(x)取最小值
时,f(x)取最小值 (14分)
(14分)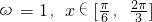 ,利用
,利用 ∥
∥ ,推出
,推出 ,然后利用两角差与和的正弦函数,化简求出tanx的值;
,然后利用两角差与和的正弦函数,化简求出tanx的值; •
• -2,根据函数f(x)的图象的相邻两个对称中心的距离为
-2,根据函数f(x)的图象的相邻两个对称中心的距离为 ,确定周期求出ω,然后求f(x)在区间
,确定周期求出ω,然后求f(x)在区间 上的最小值.
上的最小值.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com