
【题目】已知离心率为![]() 的椭圆
的椭圆![]() ,与直线
,与直线![]() 交于
交于![]() 两点,记直线
两点,记直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆方程;
(2)若![]() ,则三角形
,则三角形![]() 的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
科目:高中数学 来源: 题型:
【题目】已知动点P到两定点M(﹣3,0),N(3,0)的距离满足|PM|=2|PN|.
(1)求证:点P的轨迹为圆;
(2)记(1)中轨迹为⊙C,过定点(0,1)的直线l与⊙C交于A,B两点,求△ABC面积的最大值,并求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
如图在直三棱柱ABC—A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的
中点.
(1) 求证: AC⊥BC1
(2) 求证:AC1∥平面CDB1
(3) 求异面直线AC1与B1C所成角的余弦值.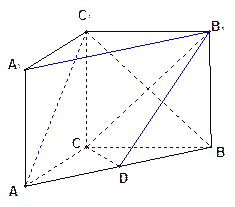
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(Ⅰ)求ω的值和f(x)的单调递增区间;
(Ⅱ)若关于x的方程f(x)﹣m=0在区间[0,![]() ]上有两个实数解,求实数m的取值范围.
]上有两个实数解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2018、2019每高考数学全国Ⅰ卷中,第22题考查坐标系和参数方程,第23题考查不等式选讲.2018年髙考结束后,某校经统计发现:选择第22题的考生较多并且得分率也较高.为研究2019年选做题得分情况,该校高三质量检测的命题完全采用2019年高考选做题模式,在测试结束后,该校数学教师对全校高三学生的选做题得分进行抽样统计,得到两题得分的统计表如下(已知每名学生只选做—道题):
第22题的得分统计表
得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 50 | 50 | 75 | 125 | 200 |
文科人数 | 25 | 25 | 125 | 0 | 25 |
第23题的得分统计表
得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 30 | 52 | 58 | 60 | 200 |
文科人数 | 5 | 10 | 10 | 5 | 70 |
(1)完成如下2×2列联表,并判断能否有99%的把握认为“选做题的选择”与“文、理科的科类”有关;
选做22题 | 选做23题 | 总计 | |
理科人数 | |||
文科人数 | |||
总计 |
(2)若以全体高三学生选题的平均得分作为决策依据,如果你是考生,根据上面统计数据,你会选做哪道题,并说明理由.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿波罗尼斯(约公元前![]() 年)证明过这样一个命题:平面内到两定点距离之比为常数
年)证明过这样一个命题:平面内到两定点距离之比为常数![]() 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点![]() 、
、![]() 间的距离为
间的距离为![]() ,动点
,动点![]() 满足
满足![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,如果存在正整数
,如果存在正整数![]() ,使得
,使得![]() 对一切
对一切![]() ,
,![]() 都成立,则称数列
都成立,则称数列![]() 为
为![]() 等差数列.
等差数列.
(1)若数列![]() 为2-等差数列,且前四项分别为2,-1,4,-3,求
为2-等差数列,且前四项分别为2,-1,4,-3,求![]() 的值;
的值;
(2)若![]() 既是2-等差数列,又是3-等差数列,证明:
既是2-等差数列,又是3-等差数列,证明:![]() 是等差数列.
是等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com