
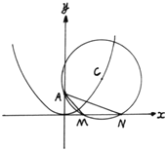
【题目】如图,已知![]() 过点
过点![]() ,圆心C在抛物线
,圆心C在抛物线![]() 上运动,若MN为
上运动,若MN为![]() 在x轴上截得的弦,设
在x轴上截得的弦,设![]() ,
,![]() ,
,![]()
![]() 当C运动时,
当C运动时,![]() 是否变化?证明你的结论.
是否变化?证明你的结论.
![]() 求
求![]() 的最大值,并求出取最大值时
的最大值,并求出取最大值时![]() 值及此时
值及此时![]() 方程.
方程.
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,且
为等差数列,且![]() ,其前8项和为52,
,其前8项和为52, ![]() 是各项均为正数的等比数列,且满足
是各项均为正数的等比数列,且满足![]() ,
, ![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意正整数
,若对任意正整数![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张在淘宝网上开一家商店,他以10元每条的价格购进某品牌积压围巾2000条.定价前,小张先搜索了淘宝网上的其它网店,发现:![]() 商店以30元每条的价格销售,平均每日销售量为10条;
商店以30元每条的价格销售,平均每日销售量为10条;![]() 商店以25元每条的价格销售,平均每日销售量为20条.假定这种围巾的销售量
商店以25元每条的价格销售,平均每日销售量为20条.假定这种围巾的销售量![]() (条)是售价
(条)是售价![]() (元)
(元)![]() 的一次函数,且各个商店间的售价、销售量等方面不会互相影响.
的一次函数,且各个商店间的售价、销售量等方面不会互相影响.
(1)试写出围巾销售每日的毛利润![]() (元)关于售价
(元)关于售价![]() (元)
(元)![]() 的函数关系式(不必写出定义域),并帮助小张定价,使得每日的毛利润最高(每日的毛利润为每日卖出商品的进货价与销售价之间的差价);
的函数关系式(不必写出定义域),并帮助小张定价,使得每日的毛利润最高(每日的毛利润为每日卖出商品的进货价与销售价之间的差价);
(2)考虑到这批围巾的管理、仓储等费用为200元/天(只要围巾没有售完,均须支付200元/天,管理、仓储等费用与围巾数量无关),试问小张应该如何定价,使这批围巾的总利润最高(总利润=总毛利润-总管理、仓储等费用)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() ,
,![]() 时,求满足
时,求满足![]() 的
的![]() 的值;
的值;
(2)若函数![]() 是定义在
是定义在![]() 上的奇函数.
上的奇函数.
①存在![]() ,使得不等式
,使得不等式![]() 有解,求实数
有解,求实数![]() 的取值范围;
的取值范围;
②若函数![]() 满足
满足![]() ,若对任意
,若对任意![]() 且
且![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十一黄金小长假期间,某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满。当每个房间每天的房价每增加10元时,就会有一个房间空闲。宾馆需对游客居住的每个房间每天支出20元的各种费用(人工费,消耗费用等等)。受市场调控,每个房间每天的房价不得高于340元。设每个房间的房价每天增加x元(x为10的正整数倍)。
(1) 设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2) 设宾馆一天的利润为w元,求w与x的函数关系式;
(3) 一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com