
【题目】在极坐标系中,直线l:![]() ,P为直线l上一点,且点P在极轴上方
,P为直线l上一点,且点P在极轴上方![]() 以OP为一边作正三角形
以OP为一边作正三角形![]() 逆时针方向
逆时针方向![]() ,且
,且![]() 面积为
面积为![]() .
.
![]() 求Q点的极坐标;
求Q点的极坐标;
![]() 求
求![]() 外接圆的极坐标方程,并判断直线l与
外接圆的极坐标方程,并判断直线l与![]() 外接圆的位置关系.
外接圆的位置关系.
科目:高中数学 来源: 题型:
【题目】某校为研究学生语言学科的学习情况,现对高二200名学生英语和语文某次考试成绩进行抽样分析.将200名学生编号为001,002,…,200,采用系统抽样的方法等距抽取10名学生,将10名学生的两科成绩(单位:分)绘成折线图如下:
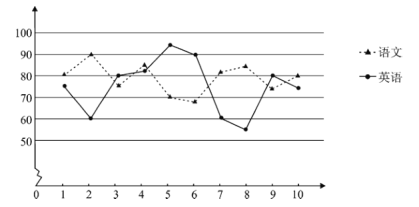
(1)若第二段抽取的学生编号是026,写出第六段抽取的学生编号;
(2)在这两科成绩差低于20分的学生中随机抽取2人进行访谈,求2人成绩均是语文成绩高于英语成绩的概率;
(3)根据折线图,比较该校高二年级学生的语文和英语两科成绩,写出至少两条统计结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,侧棱
是矩形,侧棱![]() 底面
底面![]() ,且
,且![]() ,过棱
,过棱![]() 的中点
的中点![]() ,作
,作![]() 交
交![]() 于点
于点![]() .
.
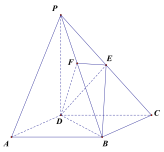
(1)证明:![]() 平面
平面![]() ;
;
(2)若面![]() 与面
与面![]() 所成二面角的大小为
所成二面角的大小为![]() ,求
,求![]() 与面
与面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
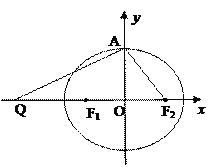
【题目】如图,设椭圆![]() 的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且
的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且![]() 0,若过 A,Q,F2三点的圆恰好与直线
0,若过 A,Q,F2三点的圆恰好与直线![]() 相切,过定点 M(0,2)的直线
相切,过定点 M(0,2)的直线![]() 与椭圆C交于G,H两点(点G在点M,H之间).(Ⅰ)求椭圆C的方程;(Ⅱ)设直线
与椭圆C交于G,H两点(点G在点M,H之间).(Ⅰ)求椭圆C的方程;(Ⅱ)设直线![]() 的斜率
的斜率![]() ,在x轴上是否存在点P(
,在x轴上是否存在点P(![]() ,0),使得以PG,PH为邻边的平行四边形是菱形?如果存在,求出
,0),使得以PG,PH为邻边的平行四边形是菱形?如果存在,求出![]() 的取值范围;如果不存在,请说明理由;(Ⅲ)若实数
的取值范围;如果不存在,请说明理由;(Ⅲ)若实数![]() 满足
满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古印度“汉诺塔问题”:一块黄铜平板上装着![]() 三根金铜石细柱,其中细柱
三根金铜石细柱,其中细柱![]() 上套着个大小不等的环形金盘,大的在下、小的在上.将这些盘子全部转移到另一根柱子上,移动规则如下:一次只能将一个金盘从一根柱子转移到另外一根柱子上,不允许将较大盘子放在较小盘子上面.若
上套着个大小不等的环形金盘,大的在下、小的在上.将这些盘子全部转移到另一根柱子上,移动规则如下:一次只能将一个金盘从一根柱子转移到另外一根柱子上,不允许将较大盘子放在较小盘子上面.若![]() 柱上现有
柱上现有![]() 个金盘(如图),将
个金盘(如图),将![]() 柱上的金盘全部移到
柱上的金盘全部移到![]() 柱上,至少需要移动次数为( )
柱上,至少需要移动次数为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的方程为
的方程为![]() ,以极点为原点,极轴所在直线为
,以极点为原点,极轴所在直线为![]() 轴建立直角坐标,直线
轴建立直角坐标,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),
为参数),![]() 与
与![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设点![]() ;若
;若![]() 、
、![]() 、
、![]() 成等比数列,求
成等比数列,求![]() 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com