
����Ŀ���������ҹ�����ȱˮ�ij���֮һ��Ϊ�˳�������Լ��ˮ���������𡱣�С����������ѧУ��2000��ͬѧ�У����������40��ͬѧ��ͥ��һ����¾���ˮ������λ���֣��������¾���ˮ����Ϊ6�飺[2��4����[4��6����[6��8����[8��10����[10��12����[12��14]����ͳ�ƣ��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ�� 
������ͼ��ʵ��a��ֵ��
�������������ݣ�����С������ѧУ2000��ͬѧ��ͥ�У��¾���ˮ������8�ֵ�Լ�ж��ٻ���
�������¾���ˮ�����ڻ����10�ֵ����������У�С�����������ȡ2��ͬѧ��ͥ���з�̸������2��ͬѧ��ǡ��1�����ڼ�ͥ���¾���ˮ������[10��12����ĸ��ʣ�
���𰸡��⣺������Ϊ�����Ƶ��֮��Ϊ1��
�����¾���ˮ��������[10��12����Ƶ��Ϊ1����0.025��2+0.075+0.100+0.225����2=0.1��
���ԣ�ͼ��ʵ��a=0.1��2=0.050��
������ͼ��֪�������������¾���ˮ������8�ֵ�Ƶ��Ϊ��0.025+0.075+0.225����2=0.65����
����С������ѧУ2000��ͬѧ��ͥ�У��¾���ˮ������8�ֵ�Լ��0.65��2000=1300��������
�����衰��2��ͬѧ��ǡ��1�����ڼ�ͥ���¾���ˮ������[10��12���顱Ϊ�¼�A��
��ͼ��֪�������������¾���ˮ����[10��12���Ļ���Ϊ0.050��2��40=4��
��������ͬѧ��ͥ�ֱ�Ϊa��b��c��d��
�¾���ˮ����[12��14]�Ļ���Ϊ0.025��2��40=2����������ͬѧ��ͥ�ֱ�Ϊe��f��
��ѡȡ��ͬѧ��ͥ�����п��ܽ��Ϊ��
��a��b������a��c������a��d������a��e������a��f������b��c������b��d������b��e����
��b��f������c��d������c��e������c��f������d��e������d��f������e��f������15�֣�����9�֣�
�¼�A�Ŀ��ܽ��Ϊ��
��a��e������a��f������b��e������b��f������c��e������c��f������d��e������d��f������8�֣�����11�֣�
������2��ͬѧ��ǡ��1�����ڼ�ͥ���¾���ˮ������[10��12����ĸ��� ![]() ��
��
�������������ɸ����Ƶ��֮��Ϊ1������¾���ˮ��������[10��12����Ƶ�ʣ��ɴ������ͼ��ʵ��a��ֵ��������������������¾���ˮ������8�ֵ�Ƶ��Ϊ0.65���ɴ������С������ѧУ2000��ͬѧ��ͥ�У��¾���ˮ������8�ֵ�Լ�ж��ٻ��������衰��2��ͬѧ��ǡ��1�����ڼ�ͥ���¾���ˮ������[10��12���顱Ϊ�¼�A����ͼ��֪�������������¾���ˮ����[10��12���Ļ���Ϊ4����������ͬѧ��ͥ�ֱ�Ϊa��b��c��d���¾���ˮ����[12��14]�Ļ���Ϊ2����������ͬѧ��ͥ�ֱ�Ϊe��f�������оٷ��������2��ͬѧ��ǡ��1�����ڼ�ͥ���¾���ˮ������[10��12����ĸ��ʣ�
�����㾫����������Ŀ����֪����������Ƶ�ʷֲ�ֱ��ͼ�����֪ʶ���Եõ�����Ĵ𰸣���Ҫ����Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ڵ�������CDEF�У�DE=CD= ![]() ��EF=2+
��EF=2+ ![]() ����������������AD��CB�۵�����ͼ��2����ʾ������E��ABCD��E��F�غϣ���
����������������AD��CB�۵�����ͼ��2����ʾ������E��ABCD��E��F�غϣ��� 
��1����֤��BE��DE��
��2�����MΪ�߶�AB���е㣬�����߶�CE��ȷ��һ��N��ʹ��MN��ƽ��DAE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�����ϡ��С����ְ��215�ˣ����������ְ��80�ˣ������ְ�������������ְ��������2����Ϊ�˽��ְ������״�����ֲ��÷ֲ�����������е��飬�ڳ�ȡ��������������ְ��16�ˣ���������е������ְ������Ϊ�� ��
A.6
B.8
C.9
D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һλͬѧ���ﶩ��һ�ݱ�ֽ���ͱ���ÿ�춼��������5��20��6��40֮�佫��ֽ�͵����ͬѧ�İְ���Ҫ����6��00��7��00֮�����ȥ�ϰ࣬����λͬѧ�İְ����뿪��ǰ���õ���ֽ�ĸ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��l��������y2=2x�ཻ��A��x1 �� y1����B��x2 �� y2�����㣬��x���ཻ�ڵ�M����y1y2=��4�� 
��1����M������ꣻ
��2����֤��OA��OB��
��3�����AOB���������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��x��R���IJ��ֶ�Ӧֵ�����
x | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | 4 |
y | ��6 | 0 | 4 | 6 | 6 | 4 | 0 | ��6 |
��һԪ���β���ʽax2+bx+c��0�Ľ⼯�ǣ� ��
A.{x|x����2����x��3}
B.{x|x�ܩ�2����x��3}
C.{x|��2��x��3}
D.{x|��2��x��3}
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����ABCDΪ�����Σ���E����PA���е㣬PB=PD��ƽ��BDE��ƽ��ABCD�� 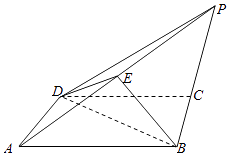
������֤��PC��ƽ��BDE��
������֤��PC��ƽ��ABCD��
������PC=��AB�����ж�ƽ��PAD��ƽ��PAB�ܷ��������������д���˵�һ��ֵ��ֻ��д�����ۣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ƽ��������ABCD��A1B1C1D�У�AB=AD=AA1=1����BAD=90�㣬��BAA1=��DAA1=60�㣬��CA1�ij�= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������A={x|a��1��x��2a+1}��B={x|0��x��1}����A��B=����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com