练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】等比数列{an}的各项均为正数，且a5a6+a4a7=18，则log3a1+log3a2+…+log3a10=（ ）
    A.5
    B.9
    C.log345
    D.10

    【答案】D
    【解析】解：依题意当n≤10时，a11﹣nan=a1q11﹣n﹣1a1qn﹣1= q9为定值， 又∵a5a6+a4a7=18，
    ∴a4a7=9，
    ∴log3a1+log3a2+…+log3a10
    =log3a1a10+log3a2a9+log3a3a8+log3a4a7+log3a5a6
    =5log3a4a7
    =5log39
    =10，
    故选：D．
    利用等比中项、对数性质可知log3a1+log3a2+…+log3a10=5log3a4a7 ， 进而计算可得结论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】阅读如图程序框图，运行相应的程序，则程序运行后输出的结果为（ ）
    A.7
    B.9
    C.10
    D.11

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，底面ABCD为菱形，E为棱PB的中点，O为AC与BD的交点，
    （Ⅰ）证明：PD∥平面EAC
    （Ⅱ）证明：平面EAC⊥平面PBD．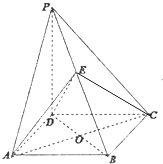

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在正三棱柱ABC﹣A1B1C1中，点D在边BC上，AD⊥C1D．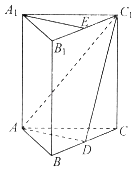
    （1）求证：平面ADC1⊥平面BCC1B1；
    （2）如果点E是B1C1的中点，求证：AE∥平面ADC1 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设Sn是数列{an}的前n项和，已知a1=3，an+1=2Sn+3（n∈N）
    （I）求数列{an}的通项公式；
    （Ⅱ）令bn=（2n﹣1）an ， 求数列{bn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个样本M的数据是x1 ， x2 ， ，xn ， 它的平均数是5，另一个样本N的数据x12 ， x22 ， ，xn2它的平均数是34．那么下面的结果一定正确的是（ ）
    A.SM2=9
    B.SN2=9
    C.SM2=3
    D.Sn2=3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 =（1，2）， =（﹣3，2）， 当k=时，（1）k + 与 ﹣3 垂直；
    当k=时，（2）k + 与 ﹣3 平行．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ax+bx（a＞0，b＞0，a≠1，b≠1）． （Ⅰ）设 ，求方程f（x）=2的根；
    （Ⅱ）设 ，函数g（x）=f（x）﹣2，已知b＞3时存在x0∈（﹣1，0）使得g（x0）＜0．若g（x）=0有且只有一个零点，求b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}满足a2=3，a3+a5=2
    （1）求{an}的通项公式；
    （2）求{an}的前n项和Sn及Sn的最大值．

    查看答案和解析>>

    同步练习册答案