【题目】为了迎接第二届国际互联网大会，组委会对报名参加服务的
名志愿者进行互联网知识测试，从这
名志愿者中采用随机抽样的方法抽取
人，所得成绩如下： 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
.
（1）作出抽取的
人的测试成绩的茎叶图，以频率为概率，估计这
志愿者中成绩不低于
分的人数；
（2）从抽取的成绩不低于
分的志愿者中，随机选
名参加某项活动，求选取的
人恰有一人成绩不低于
分的概率.
【答案】(1) 
；(2) 
.
【解析】试题分析：（Ⅰ）根据成绩，茎为十位数字5,6,7,8,9，个数数字为叶，得茎叶图，由样本得成绩在90以上频率为
，由此可估计出成绩不低于90分的人数；（Ⅱ）抽取的成绩不低于80分的志愿者有6人，从中选3人可有20种选法（可用列举法列出各种可能），然后再数出恰有一人成绩不低于90分的有12种，由概率公式可得概率．
试题解析：（Ⅰ）抽取的15人的成绩茎叶图如图所示，
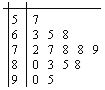
由样本得成绩在90以上频率为
，故志愿者测试成绩在90分以上（包含90分）的人数约为
=200人.
（Ⅱ）设抽取的15人中，成绩在80分以上（包含80分）志愿者为
, 
, 
, 
, 
, 
,其中
， 
的成绩在90分以上（含90分），
成绩在80分以上（包含80分）志愿者中随机选3名志愿者的不同选法有：{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
, 
, 
},{ 
, 
, 
},{ 
, 
, 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
},{ 
， 
， 
}共20种，
其中选取的3人中恰有一人成绩在90分以上的不同取法有：{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
, 
, 
},{ 
, 
, 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}共12种，
∴选取的3人中恰有一人成绩在90分以上的概率为
=
.
科目：高中数学 来源： 题型：
【题目】下列事件是随机事件的是（ ）
①当x>10时，
； ②当x∈R，x2+x＝0有解
③当a∈R关于x的方程x2+a＝0在实数集内有解； ④当sinα>sinβ时，α>β（ ）
A.①②B.②③C.③④D.①④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在对人们的休闲方式的一次调查中，用简单随机抽样方法调查了125人，其中女性70人，男性55人.女性中有40人主要的休闲方式是看电视，另外30人主要的休闲方式是运动；男性中有20人主要的休闲方式是看电视，另外35人主要的休闲方式是运动.
（1）根据以上数据建立一个
列联表；
（2）能否在犯错误的概率不超过0.025的前提下，认为性别与休闲方式有关系?
（3）在休闲方式为看电视的人中按分层抽样方法抽取6人参加某机构组织的健康讲座，讲座结束后再从这6人中抽取2人作反馈交流，求参加交流的恰好为2位女性的概率.
附：
P（ | 0.05 | 0.025 | 0.010 |
k | 3.841 | 5.024 | 6.635 |
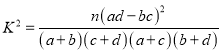
休闲方式 性别 | 看电视 | 运动 | 合计 |
女 | |||
男 | |||
合计 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在某区“创文明城区”（简称“创城”）活动中，教委对本区
四所高中学校按各校人数分层抽样，随机抽查了100人，将调查情况进行整理后制成下表：
学校 |
|
|
|
|
抽查人数 | 50 | 15 | 10 | 25 |
“创城”活动中参与的人数 | 40 | 10 | 9 | 15 |
（注：参与率是指：一所学校“创城”活动中参与的人数与被抽查人数的比值）假设每名高中学生是否参与”创城”活动是相互独立的.
（1）若该区共2000名高中学生，估计
学校参与“创城”活动的人数；
（2）在随机抽查的100名高中学生中，随机抽取1名学生，求恰好该生没有参与“创城”活动的概率；
（3）在上表中从
两校没有参与“创城”活动的同学中随机抽取2人，求恰好两校各有1人没有参与“创城”活动的概率是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
