练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在正方体ABCD﹣A1B1C1D1中，E是A1B1上一点，若平面EBD与平面ABCD所成锐二面角的正切值为 ，设三棱锥A﹣A1D1E外接球的直径为a，则 = ．

    【答案】
    【解析】解：过E作EF∥AA1交AB于F，过F作FG⊥BD于G，连接EG，则∠EGF为平面EBD与平面AB﹣CD所成锐二面角的平面角，∵ ，∴ ，

    设AB=3，则EF=3，∴ ，则BF=2=B1E，

    ∴A1E=1，则三棱锥A﹣A1D1E外接球的直径 ，

    ∴ ．

    所以答案是 ．

    【考点精析】认真审题，首先需要了解棱柱的结构特征(两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形)，还要掌握球内接多面体(球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长)的相关知识才是答题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知圆心在直线上的圆经过点，但不经过坐标原点，并且直线与圆相交所得的弦长为4.

    （1）求圆的一般方程；

    （2）若从点发出的光线经过轴反射，反射光线刚好通过圆的圆心，求反射光线所在的直线方程（用一般式表达）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了调查喜欢旅游是否与性别有关，调查人员就“是否喜欢旅游”这个问题，在火车站分别随机调研了50名女性和50名男性，根据调研结果得到如图所示的等高条形图
    （Ⅰ）完成下列2×2列联表：

    喜欢旅游

    不喜欢旅游

    合计

    女性

    男性

    合计

    （II）能否在犯错率不超过0.025的前提下认为“喜欢旅游与性别有关”
    附：

    P（K2≥k0）

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    k0

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    （参考公式：K2= ，其中n=a+b+c+d）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 的图像如图所示.

    （1）求函数的解析式；

    （2）当时，求函数的最大值和最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形ABCD是矩形，MD⊥平面ABCD，NB∥MD，且AD=2，NB=1，CD=MD=3．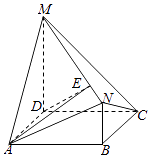

    （1）过B作平面BFG∥平面MNC，平面BFG与CD、DM分别交于F、G，求AF与平面MNC所成角的正弦值；
    （2）E为直线MN上一点，且平面ADE⊥平面MNC，求 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点是圆内一点，直线.

    （1）若圆的弦恰好被点平分，求弦所在直线的方程；

    （2）若过点作圆的两条互相垂直的弦，求四边形的面积的最大值；

    （3）若， 是上的动点，过作圆的两条切线，切点分别为.证明：直线过定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数满足，且的最小值是.

    （1）求的解析式；

    （2）若关于的方程在区间上有唯一实数根，求实数的取值范围；

    （3）函数，对任意都有恒成立，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案