
【题目】已知函数f(x)=ex+ax2+bx(e为自然对数的底,a,b为常数),曲线y=f(x)在x=0处的切线经过点A(﹣1,﹣1)
(1)求实数b的值;
(2)是否存在实数a,使得曲线y=f(x)所有切线的斜率都不小于2?若存在,求实数a的取值集合,若不存在,说明理由.
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
【题目】为弘扬民族古典文化,市电视台举行古诗词知识竞赛,某轮比赛由节目主持人随机从题库中抽取题目让选手抢答,回答正确将给该选手记正10分,否则记负10分.根据以往统计,某参赛选手能答对每一个问题的概率均为![]() ;现记“该选手在回答完
;现记“该选手在回答完![]() 个问题后的总得分为
个问题后的总得分为![]() ”.
”.
(1)求![]() 且
且![]() (
(![]() )的概率;
)的概率;
(2)记![]() ,求
,求![]() 的分布列,并计算数学期望
的分布列,并计算数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A(﹣2,0),B(2,0),P为不在x轴上的动点,直线PA,PB的斜率满足kPAkPB![]() .
.
(1)求动点P的轨迹Γ的方程;
(2)若M,N是轨迹Γ上两点,kMN=1,求△OMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
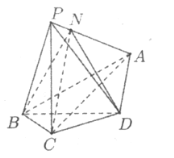
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在,求出线段
,若存在,求出线段![]() 的长,若不存在,说明理由.
的长,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市从2014年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,并按[ 0,10],(10,20],(20,30],(30,40],(40,50]分组,得到频率分布直方图如下:
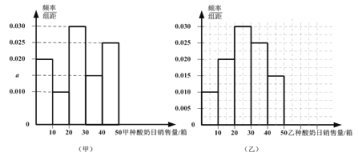
假设甲、乙两种酸奶独立销售且日销售量相互独立.
(1)写出频率分布直方图(甲)中的![]() 的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为
的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(2)估计在未来的某一天里,甲、乙两种酸奶的销售量恰有一个高于20箱且另一个不高于20箱的概率;
(3)设![]() 表示在未来3天内甲种酸奶的日销售量不高于20箱的天数,以日销售量落入各组的频率作为概率,求
表示在未来3天内甲种酸奶的日销售量不高于20箱的天数,以日销售量落入各组的频率作为概率,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com