
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由函数f(x)是定义在R上的奇函数,∴可得(-x)=-f(x),其图象关于原点对称,在对称区间单调性相同,对选项逐一判定即可.
解答 解:∵函数f(x)是定义在R上的奇函数,∴f(-x)=-f(x),其图象关于原点对称,在对称区间单调性相异;
对于(1),f(-0)=-f(0)⇒f(0)=0,故正确;
对于(2),f(-2)=-f(2)⇒f(2)=-1,故错;
对于(3),因为奇函数的图象关于原点对称,所以若f(x)在[1,+∞)上为减函数,则f(x)在(-∞,-1]上为减函数,故错;
对于(4),其图象关于原点对称,f(x)在(0,+∞)上有最小值-m,则f(x)在(-∞,0)上有最大值m,故正确;
故选:B.
点评 本题考查了,奇函数的图象及性质,属于基础题.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 0 | 1 | 2 |
| y | a | $\frac{20}{3}$ | $\frac{40}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
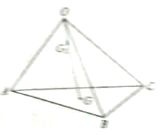
| A. | $\overrightarrow{O{G_1}}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$ | B. | $\overrightarrow{O{G_1}}=\frac{1}{9}\overrightarrow{OA}+\frac{1}{9}\overrightarrow{OB}+\frac{1}{9}\overrightarrow{OC}$ | ||
| C. | $\overrightarrow{O{G_1}}=\frac{1}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$ | D. | $\overrightarrow{O{G_1}}=\frac{3}{4}\overrightarrow{OA}+\frac{3}{4}\overrightarrow{OB}+\frac{3}{4}\overrightarrow{OC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com