
【题目】设![]() ,对于
,对于![]() ,有
,有![]() .
.
(1)证明:![]()
(2)令![]() ,
,
证明 :(I)当![]() 时,
时,![]()
(II)当![]() 时,
时,![]()
【答案】(1)见解析;(2)(I)见解析;(II)见解析.
【解析】
(1)由分析法可证明,找到![]() 成立的充分性。(2)(I)当
成立的充分性。(2)(I)当![]() 时,当
时,当![]() 时,有
时,有![]() ;再由分析法证明
;再由分析法证明![]() 。(II)当
。(II)当![]() 时,当
时,当![]() 时,有
时,有![]() ,再由分析法结合数学归纳法证明
,再由分析法结合数学归纳法证明![]() 。
。
(1)若![]() ,则只需证
,则只需证![]()
![]()
只需证![]() 成立
成立
只需要证![]() 成立,而该不等式在
成立,而该不等式在![]() 时恒成立…
时恒成立…
故只需要验证![]() 时成立即可,
时成立即可,
而当![]() 时,
时,![]() 均满足该不等式。
均满足该不等式。
综上所得不等式![]() 成立。
成立。
(2)、(I)当![]() 时,
时,
用数学归纳法很明显可证当![]() 时,有
时,有![]() ;
;
下证:![]() ,
,
只需要证![]() ,
,
只需证![]()
只需证![]() ,
,
只需证![]() ,
,
只需证![]() .
.
由(1)可知,我们只需要证![]() ,
,
只需证![]() ,只需证
,只需证![]() .
.
当![]() 时该不等式恒成立
时该不等式恒成立
当![]() 时,
时,![]()
![]()
![]() ,故该不等式恒成立
,故该不等式恒成立
综上所得,上述不等式![]() 成立
成立
(II)、当![]() 时,用数学归纳法很明显可证当
时,用数学归纳法很明显可证当![]() 时,有
时,有![]()
下证:![]()
只需证: ![]() ,
,
只需证:![]()
只需证:![]() ,
,
只需证:![]()
只需证:![]() ,……
,……
同理由(2)及数学归纳法,可得该不等式成立。
综上所述,不等式![]() 成立
成立


科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() .
.
(1)当![]() 时,求
时,求![]() 的极值;
的极值;
(2)当![]() 时,若函数
时,若函数![]() 恰有两个不同的零点,求
恰有两个不同的零点,求![]() 的值;
的值;
(3)当![]() 时,若
时,若![]() 的解集为
的解集为![]() ,且
,且![]() 中有且仅有一个整数,求实数
中有且仅有一个整数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,
上,![]() 平面
平面![]() ,
,![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
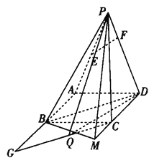
(1)证明:![]() 平面
平面![]() .
.
(2)过点![]() 作
作![]() 的平行线,与直线
的平行线,与直线![]() 相交于点
相交于点![]() ,点
,点![]() 为
为![]() 的中点,求
的中点,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的各项为正数,且
的各项为正数,且![]() ,数列
,数列![]() 满足:
满足:![]() 对任意
对任意![]() 恒成立,且常数
恒成立,且常数![]() .
.
(1)若![]() 为等差数列,求证:
为等差数列,求证:![]() 也为等差数列;
也为等差数列;
(2)若![]() ,
,![]() 为等比数列,求
为等比数列,求![]() 的值(用c表示);
的值(用c表示);
(3)若![]() 且
且![]() ,令
,令![]() ,求证
,求证![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,圆
轴正半轴为极轴的极坐标系中,圆![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在班级活动中,4名男生和3名女生站成一排表演节目:(写出必要的数学式,结果用数字作答)
(1)三名女生不能相邻,有多少种不同的站法?
(2)四名男生相邻有多少种不同的排法?
(3)女生甲不能站在左端,女生乙不能站在右端,有多少种不同的排法?
(4)甲乙丙三人按高低从左到右有多少种不同的排法?(甲乙丙三位同学身高互不相等)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题
①“若![]() ,则互为相反数”的逆命题;
,则互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若![]() ,则
,则![]() 有实根”的逆否命题;
有实根”的逆否命题;
④“不等边三角形的三个内角相等”的逆命题.
其中真命题为_______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点
的一个焦点![]() ,两个焦点与短轴的一个端点构成等边三角形.
,两个焦点与短轴的一个端点构成等边三角形.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过焦点![]() 作
作![]() 轴的垂线交椭圆上半部分于点
轴的垂线交椭圆上半部分于点![]() ,过点
,过点![]() 作椭圆
作椭圆![]() 的弦
的弦![]() ,设弦
,设弦![]() 所在的直线分别交
所在的直线分别交![]() 轴于
轴于![]() 、
、![]() 两点,若
两点,若![]() 为等腰三角形时,问直线
为等腰三角形时,问直线![]() 的斜率是否为定值?若是,求出这个定值;若不是,请说明理由.
的斜率是否为定值?若是,求出这个定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com