
【题目】下列命题:①在线性回归模型中,相关指数![]() 表示解释变量
表示解释变量![]() 对于预报变量
对于预报变量![]() 的贡献率,
的贡献率, ![]() 越接近于1,表示回归效果越好;②两个变量相关性越强,则相关系数的绝对值就越接近于1;③在回归直线方程
越接近于1,表示回归效果越好;②两个变量相关性越强,则相关系数的绝对值就越接近于1;③在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均减少0.5个单位;④对分类变量
平均减少0.5个单位;④对分类变量![]() 与
与![]() ,它们的随机变量
,它们的随机变量![]() 的观测值
的观测值![]() 来说,
来说, ![]() 越小,“
越小,“![]() 与
与![]() 有关系”的把握程度越大.其中正确命题的个数是( )
有关系”的把握程度越大.其中正确命题的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响,已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用![]() 表示该学生选修的课程门数和没有选修的课程门数的乘积.
表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数![]() 为
为![]() 上的偶函数”为事件
上的偶函数”为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(2)求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,三边a,b,c所对的角分别为A,B,C,设函数f(x)=![]() sin2x+cos2x,且f(
sin2x+cos2x,且f(![]() )=2.
)=2.
(1)若acosB+bcosA=csinC,求角B的大小;
(2)记g(λ)=|![]() +λ
+λ![]() |,若|
|,若|![]() |=|
|=|![]() |=3,试求g(λ)的最小值.
|=3,试求g(λ)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(1-2x)(x2-2).
(1)求f(x)的单调区间和极值;
(2)若直线y=4x+b是函数y=f(x)图象的一条切线,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)上一点P(3,t)到其焦点的距离为4.
(1)求p的值;
(2)过点Q(1,0)作两条直线l1 , l2与抛物线分别交于点A、B和C、D,点M,N分别是线段AB和CD的中点,设直线l1 , l2的斜率分别为k1 , k2 , 若k1+k2=3,求证:直线MN过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中:
①若![]() ,满足
,满足![]() ,则
,则![]() 的最大值为4;
的最大值为4;
②若![]() ,则函数
,则函数![]() 的最小值为3;
的最小值为3;
③若![]() ,满足
,满足![]() ,则
,则![]() 的最大值为
的最大值为![]() ;
;
④若![]() ,满足
,满足![]() ,则
,则![]() 的最小值为2;
的最小值为2;
⑤函数![]() 的最小值为9.
的最小值为9.
正确的有________.(把你认为正确的序号全部写上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的通项为an=log(n+1)(n+2)(n∈N*),我们把使乘积a1a2a3…an为整数的n叫做“优数”,则在(0,2015]内的所有“优数”的和为( )
A.1024
B.2012
C.2026
D.2036
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人们生活水平的不断提高,家庭理财越来越引起人们的重视.某一调查机构随机调查了5个家庭的月收入与月理财支出(单位:元)的情况,如下表所示:
月收入 | 8 | 10 | 9 | 7 | 11 |
月理财支出 |
|
|
|
|
|
(I)在下面的坐标系中画出这5组数据的散点图;
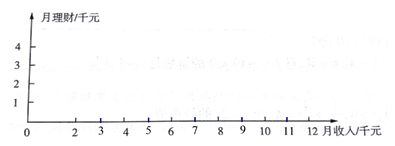
(II)根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(III)根据(II)的结果,预测当一个家庭的月收入为![]() 元时,月理财支出大约是多少元?
元时,月理财支出大约是多少元?
(附:回归直线方程![]() 中,
中,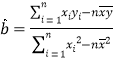 ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《孙子算经》中有如下问题:“今有三女,长女五日一归,中女四日一归,少女三日一归.问:三女何日相会?” 意思是:“一家出嫁的三个女儿中,大女儿每五天回一次娘家,二女儿每四天回一次娘家,小女儿每三天回一次娘家.三个女儿从娘家同一天走后,至少再隔多少天三人再次相会?”假如回娘家当天均回夫家,若当地风俗正月初二都要回娘家,则从正月初三算起的一百天内,有女儿回娘家的天数有
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com