
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,且过点
,且过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若不经过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,且直线
两点,且直线![]() 与直线
与直线![]() 的斜率之和为
的斜率之和为![]() ,证明:直线
,证明:直线![]() 的斜率为定值.
的斜率为定值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由已知条件先求出椭圆![]() 的半焦距,再把
的半焦距,再把![]() 代入椭圆方程,结合性质
代入椭圆方程,结合性质![]() ,求出
,求出![]() 、
、![]() 、
、![]() ,即可求出椭圆
,即可求出椭圆![]() 的方程;(2)设直线
的方程;(2)设直线![]() 的方程为
的方程为![]() 与椭圆的方程联立,根据韦达定理及过两点的斜率公式,利用直线
与椭圆的方程联立,根据韦达定理及过两点的斜率公式,利用直线![]() 的斜率之和为零可得
的斜率之和为零可得![]() ,从而可得结果.
,从而可得结果.
试题解析:(1)因为椭圆![]() 的焦距为
的焦距为![]() ,且过点
,且过点![]() ,所以
,所以![]() .因为
.因为![]() ,解得
,解得![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() .
.
(2)设点![]() ,则
,则![]() ,由
,由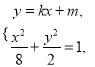 消去
消去![]() 得
得![]() ,(*)则
,(*)则![]() ,因为
,因为![]() ,即
,即![]() ,化简得
,化简得![]() .即
.即![]() .(**)代入得
.(**)代入得![]() ,整理得
,整理得![]() ,所以
,所以![]() 或
或![]() .若
.若![]() ,可得方程(*)的一个根为
,可得方程(*)的一个根为![]() ,不合题意,所以直线
,不合题意,所以直线![]() 的斜率为定值,该值为
的斜率为定值,该值为![]() .
.
【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系和过两点的斜率公式,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
乙厂:
分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面![]() 列联表,并问是否有
列联表,并问是否有![]() 的把握认为“两个分厂生产的零件的质量有差异”.
的把握认为“两个分厂生产的零件的质量有差异”.
甲 厂 | 乙 厂 | 合计 | |
优质品 | |||
非优质品 | |||
合计 |
附: 
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四棱锥S﹣ABCD中,底面ABCD是菱形,且∠BCD=60°,侧面SAB是正三角形,且面SAB⊥面ABCD,F为SD的中点. 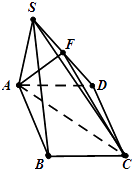
(1)证明:SB∥面ACF;
(2)求面SBC与面SAD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)过点A(﹣
=1(a>b>0)过点A(﹣ ![]() ,
, ![]() ),离心率为
),离心率为 ![]() ,点F1 , F2分别为其左右焦点.
,点F1 , F2分别为其左右焦点.
(1)求椭圆C的标准方程;
(2)若y2=4x上存在两个点M,N,椭圆上有两个点P,Q满足,M,N,F2三点共线,P,Q,F2三点共线,且PQ⊥MN.求四边形PMQN面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意的x,y∈R,总有f(x)+f(y)=f(x+y),且x<0时,f(x)>0.
(1)求证:函f(x)是奇函数;
(2)求证:函数f(x)是R上的减函数;
(3)若定义在(﹣2,2)上的函数f(x)满足f(﹣m)+f(1﹣m)<0,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出三种函数模型:f(x)=xn(n>0),g(x)=ax(a>1)和h(x)=logax(a>1).根据它们增长的快慢,则一定存在正实数x0 , 当x>x0时,就有( )
A.f(x)>g(x)>h(x)
B.h(x)>g(x)>f(x)
C.f(x)>h(x)>g(x)
D.g(x)>f(x)>h(x)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行“庆元旦”教工羽毛球单循环比赛(任意两个参赛队伍只比赛一场),有高一、高二、高三共三个队参赛,高一胜高二的概率为![]() ,高一胜高三的概率为
,高一胜高三的概率为![]() ,高二胜高三的概率为
,高二胜高三的概率为![]() ,每场胜负相互独立,胜者记1分,负者记0分,规定:积分相同时,高年级获胜.
,每场胜负相互独立,胜者记1分,负者记0分,规定:积分相同时,高年级获胜.
(1)若高三获得冠军的概率为![]() ,求
,求![]() ;
;
(2)记高三的得分为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com