
【题目】【选修4-4:坐标系与参数方程】
在平面直角坐标系![]() ,已知曲线
,已知曲线 (
(![]() 为参数),在以
为参数),在以![]() 原点为极点,
原点为极点, ![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() ,
, ![]() 两点,求点
两点,求点![]() 到
到![]() ,
, ![]() 的距离之积。
的距离之积。
科目:高中数学 来源: 题型:
【题目】某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示,其中一个数字被污损.
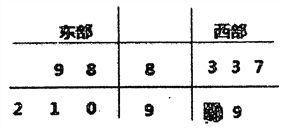
(I)求东部观众平均人数超过西部观众平均人数的概率.
(II)节目的播出极大激发了观众随机统计了4位观众的周均学习成语知识的的时间y (单位:小时)与年龄x(单位:岁),并制作了对照表(如下表所示):

由表中数据分析,x,y呈线性相关关系,试求线性回归方程![]() ,并预测年龄为60岁观众周均学习成语知识的时间.
,并预测年龄为60岁观众周均学习成语知识的时间.
参考数据:线性回归方程中![]() 的最小二乘估计分别是
的最小二乘估计分别是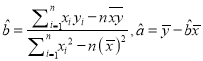 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() ,侧面
,侧面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
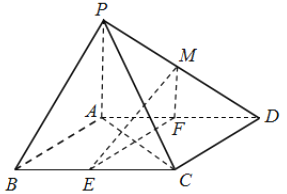
(1)求证: ![]() 平面
平面![]() ;
;
(2)如果直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市垃圾处理站每月的垃圾处理量最少为400吨,最多为600吨,月处理成本![]() (元)与月垃圾处理量
(元)与月垃圾处理量![]() (吨)之间的函数关系可近似地表示为
(吨)之间的函数关系可近似地表示为![]() ,且每处理一吨垃圾得到可利用的资源值为100元.
,且每处理一吨垃圾得到可利用的资源值为100元.
(1)该站每月垃圾处理量为多少吨时,才能使每吨垃圾的平均处理成本最低?
(2)该站每月能否获利?如果获利,求出最大利润;如果不获利,则需要市财政补贴,至少补贴多少元才能使该站不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若![]() ,证明:函数
,证明:函数![]() 在
在![]() 上单调递减;
上单调递减;
(Ⅱ)是否存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 内存在两个极值点?若存在,求实数
内存在两个极值点?若存在,求实数![]() 的取值范围;若不存在,请说明理由. (参考数据:
的取值范围;若不存在,请说明理由. (参考数据: ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
表1:甲套设备的样本的频数分布表
质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 5 | 18 | 19 | 6 | 1 |
图1:乙套设备的样本的频率分布直方图
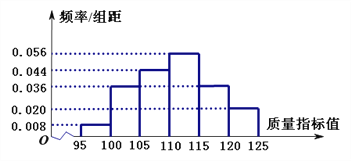
(Ⅰ)将频率视为概率. 若乙套设备生产了5000件产品,则其中的不合格品约有多少件;
(Ⅱ)填写下面列联表,并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关;
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(Ⅲ)根据表1和图1,对两套设备的优劣进行比较.
附:

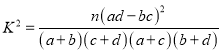 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com