练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知定义域为的函数是奇函数，且．

    （1）求a的值；

    （2）求证：在定义域上是减函数．

    （3）解关于实数的不等式．

    【答案】（1） （2）证明见解析 （3）

    【解析】

    （1）由函数是定义域为R的奇函数，得到，即可求解；

    （2）利用函数的单调的定义，即可证得函数在定义域上是减函数；

    （3）利用函数是奇函数，把不等式转化为，再利用函数的定义域和单调性，列出不等式组，即可求解.

    （1）由题意，函数是定义域为R的奇函数，所以，

    即，所以，

    经检验时，函数是奇函数，所以.

    （2）由于，所以，即，

    设，

    则，

    因为且函数在定义域上递增，

    可得，，所以，

    所以，即，

    所以在上的减函数．

    （3）由于函数是奇函数，所以，

    所以，转化成，

    则满足，解得，即不等式的解集为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】函数的定义域为，且对任意，有，且当时，，

    (Ⅰ)证明是奇函数；

    (Ⅱ)证明在上是减函数；

    (III)若,，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列集合中表示同一集合的是( )

    A.，B.，

    C.，D.，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二项式展开式中各项系数之和比各二项式系数之和大240，

    (1)求；(2)求展开式中含项的系数；(3)求展开式中所有含的有理项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设A＝{x|2x2＋ax＋2＝0}，B＝{x|x2＋3x＋2a＝0}，且A∩B＝{2}．

    (1)求a的值及集合A，B；

    (2)设全集U＝A∪B，求(UA)∪(UB)；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某学校准备修建一个面积为2400平方米的矩形活动场地（图中ABCD）的围栏，按照修建要求，中间用围墙EF隔开，使得ABEF为矩形，EFCD为正方形，设米，已知围墙（包括EF）的修建费用均为每米500元，设围墙（包括EF）的修建总费用为y元．

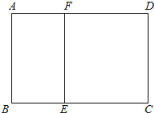
    （1）求出y关于x的函数解析式及x的取值范围；

    （2）当x为何值时，围墙（包括EF）的修建总费用y最小？并求出y的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}中an= （n∈N*），将数列{an}中的整数项按原来的顺序组成数列{bn}，则b2018的值为（ ）
    A.5035
    B.5039
    C.5043
    D.5047

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}中an= （n∈N*），将数列{an}中的整数项按原来的顺序组成数列{bn}，则b2018的值为（ ）
    A.5035
    B.5039
    C.5043
    D.5047

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，圆的参数方程为，（t为参数），在以原点O为极点，轴的非负半轴为极轴建立的极坐标系中，直线的极坐标方程为，两点的极坐标分别为．

    （1）求圆的普通方程和直线的直角坐标方程；

    （2）点是圆上任一点，求面积的最小值．

    查看答案和解析>>

    同步练习册答案